【2013一橋大学・後期】
\(e^{\pi}\) と \(\pi^e\) の大小を比較せよ.
解答・解説
\(f(x)=\displaystyle\frac{\log x}{x}\) ( \(x>0\) ) とおく.
\(f^{\prime}(x)=\displaystyle\frac{1-\log x}{x^2}\) より
\(f^{\prime}(x)=0\) とすると
\(\log x=1\) \(\iff\) \(x=e\)
| \(x\) | \(0\) | ・・・ | \(e\) | ・・・ |
| \(f^{\prime}(x)\) | + | \(0\) | ー | |
| \(f(x)\) | ↗️ | ↘️ |
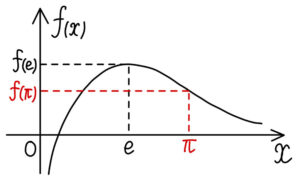
よって,\(y=f(x)\) は \(x>e\) において単調減少なグラフとなる.
\(e<\pi\) より \(f(e)>f(\pi)\)
\(\displaystyle\frac{\log e}{e}>\displaystyle\frac{\log \pi}{\pi}\)
\(\pi\log e>e\log \pi\)
\(\log e^{\pi}>\log \pi^{e}\) であるから
\(e^{\pi}>\pi^{e}\)

\(a^b\) と \(b^a\) の大小については,
\(f(x)=\displaystyle\frac{\log x}{x}\) のグラフを利用することで考えることができます!
頻出・有名入試問題ですので,流れを覚えておきましょう!!







コメント