【2021東京大学・理科・第2問】
複素数 \(a\),\(b\),\(c\) に対して整式 \(f(z)=az^2+bz+c\) を考える. \(i\) を虚数単位とする.
(1) \(\alpha\),\(\beta\),\(\gamma\) を複素数とする.\(f(0)=\alpha\),\(f(1)=\beta\),\(f(i)=\gamma\) が成り立つとき,\(a\),\(b\),\(c\) をそれぞれ \(\alpha\),\(\beta\),\(\gamma\) で表せ.
(2) \(f(0)\), \(f(1)\), \(f(i)\) がいずれも \(1\) 以上 \(2\) 以下の実数であるとき, \(f(2)\) のとりうる範囲を複素数平面上に図示せよ.
解答・解説
(1)
\(f(0)=\alpha\) より,\(c=\alpha\) ・・・①
\(f(1)=\beta\) より,\(a+b+c=\beta\)
①より,\(a+b=-\alpha+\beta\) ・・・②
\(f(i)=\gamma\) より,\(-a+ib+c=\gamma\)
①より,\(-a+ib=-\alpha+\gamma\) ・・・③
② \(\times i-\) ③より
\((1+i)a=(1-i)\alpha+i\beta-\gamma\)
\(a=\displaystyle\frac{(1-i)\alpha+i\beta-\gamma}{1+i}\)
分母分子に \(1-i\) をかけて式を整理すると
\(a=-i\alpha+\displaystyle\frac{1+i}{2}\beta-\displaystyle\frac{1-i}{2}\gamma\)
また,②+③より
\((1+i)b=-2\alpha+\beta+\gamma\)
\(b=\displaystyle\frac{-2\alpha+\beta+\gamma}{1+i}\)
よって,\(b=(-1+i)\alpha+\displaystyle\frac{1-i}{2}\beta+\displaystyle\frac{1-i}{2}\gamma\)
以上より,
\(\begin{cases} a=-i\alpha+\displaystyle\frac{1+i}{2}\beta-\displaystyle\frac{1-i}{2}\gamma \\b=(-1+i)\alpha+\displaystyle\frac{1-i}{2}\beta+\displaystyle\frac{1-i}{2}\gamma\\c=\alpha \end{cases}\)
(2)
\(f(2)=4a+2b+c\) に (1) の結果を代入すると
\(f(2)=4\left(-i\alpha+\displaystyle\frac{1+i}{2}\beta-\displaystyle\frac{1-i}{2}\gamma\right)+2\left\{(-1+i)\alpha+\displaystyle\frac{1-i}{2}\beta+\displaystyle\frac{1-i}{2}\gamma\right\}+\alpha\)
式を整理すると
\(f(2)=(-1-2i)\alpha+(3+i)\beta+(-1+i)\gamma\)
ここで,\(z_{1}=-1-2i\),\(z_{2}=3+i\),\(z_{3}=-1+I\) とおくと,
\(f(2)=\alpha z_{1}+\beta z_{2}+\gamma z_{3}\)
まず初めに,点 \(\alpha z_{1}+\beta z_{2}\) について考える.
\(1≦\alpha≦2\),\(1≦\beta≦2\) より,
点 \(\alpha z_{1}+\beta z_{2}\) の存在する領域は,\(4\) 点 \(z_{1}+z_{2}\), \(2z_{1}+z_{2}\), \(z_{1}+2z_{2}\), \(2z_{1}+2z_{2}\) を頂点とする平行四辺形の周および内部.(下図の赤斜線部)
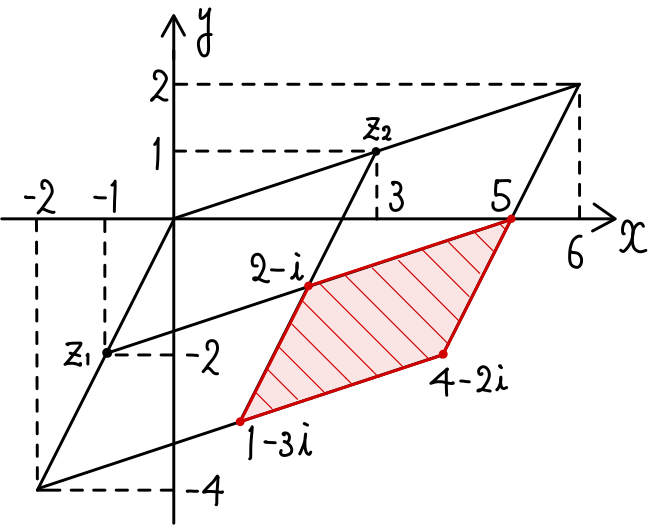
であるから,\(f(2)\) の存在する領域は,点 \(\alpha z_{1}+\beta z_{2}\) の存在する領域を \(\gamma z_{3}\) だけ動かした領域である.
\(1≦\gamma≦2\) であるので,求める領域は下図の青斜線部の周および内部となる.
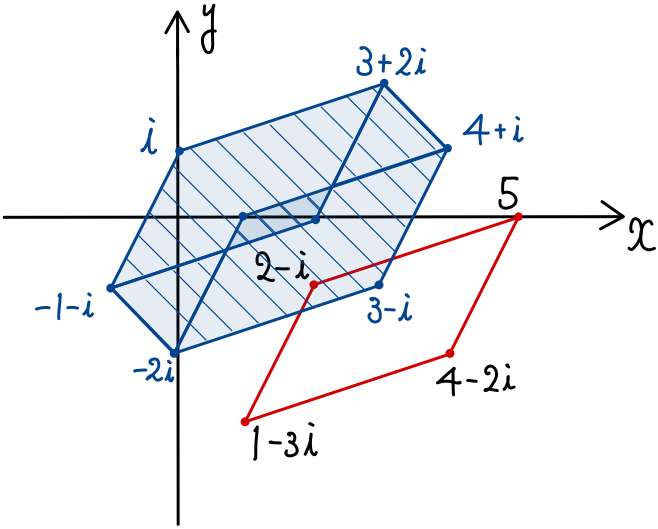







コメント