【2022大阪医科薬科大学・看護・[2]】

解答・解説
\(x^2-6x-5>0\) ・・・①,\(x^2-3kx-4k^2<0\) ・・・②
(1) \(x^2-6x-5=0\) とすると解の公式から
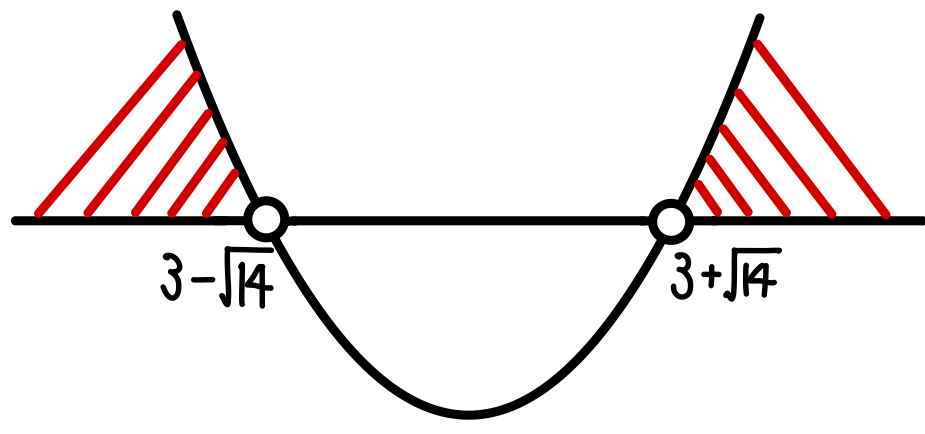 \(x=3\pm\sqrt{14}\) より
\(x=3\pm\sqrt{14}\) より
① \(\iff\) \(x<3-\sqrt{14}\) または \(3+\sqrt{14}<x\) ・・・( b )
(2) ②の解が \(-1<x<4\) のとき
\((x+1)(x-4)<0\)
\(x^2-3x-4<0\)
②と係数を比較すると,\(k=1\) ・・・( d )
(3) ② \(\iff\) \((x+k)(x-4k)<0\)
\(k>0\) より \(-k<x<4k\)
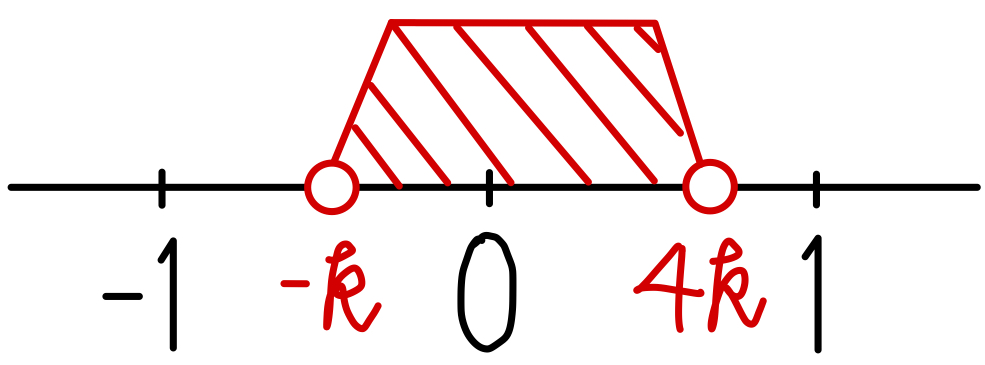
これを満たす自然数 \(x\) が存在しないとき
\(-1≦-k<0\) かつ \(0<4k≦1\)
\(\iff\) \(0<k≦1\) かつ \(0<k≦\displaystyle\frac{1}{4}\)
よって,\(0<k≦\displaystyle\frac{1}{4}\) ・・・( b )
(4) ②について
( ⅰ ) \(k>0\) のとき
② \(\iff\) \(-k<x<4k\)
①,②を同時に満たす \(x\) が存在しないとき
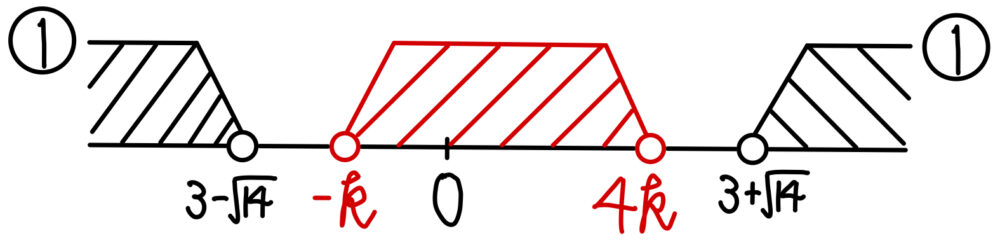
\(3-\sqrt{14}≦-k<0\) かつ \(0<4k≦3+\sqrt{14}\)
\(\iff\) \(0<k≦\sqrt{14}-3\) かつ \(0<k≦\displaystyle\frac{3+\sqrt{14}}{4}\)
ここで,
\((\sqrt{14}-3)-\displaystyle\frac{3+\sqrt{14}}{4}=\displaystyle\frac{1}{4}(3\sqrt{14}-15)\)
\(=\displaystyle\frac{1}{4}(\sqrt{126}-\sqrt{225})<0\) より
\(\sqrt{14}-3<\displaystyle\frac{3+\sqrt{14}}{4}\) なので,
② \(\iff\) \(0<k≦\sqrt{14}-3\)
( ⅱ ) \(k=0\) のとき
②を満たす実数解は存在しないので条件をみたす.
よって,\(k=0\)
( ⅲ ) \(k<0\) のとき
② \(\iff\) \(4k<x<-k\)
①,②を同時に満たす \(x\) が存在しないとき
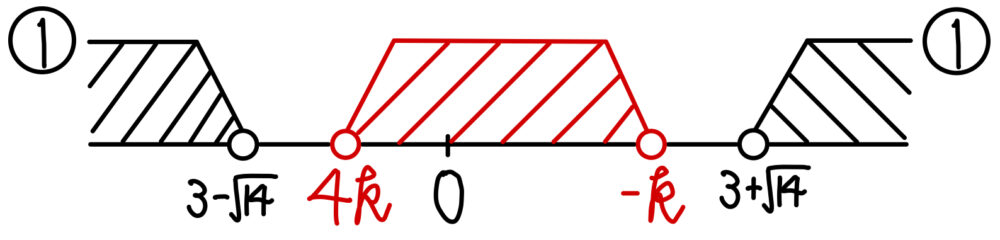
\(3-\sqrt{14}≦4k<0\) かつ \(0<-k≦3+\sqrt{14}\)
\(\iff\) \(\displaystyle\frac{3-\sqrt{14}}{4}≦k<0\) かつ \(-3-\sqrt{14}≦k<0\)
よって,\(\displaystyle\frac{3-\sqrt{14}}{4}≦k<0\)
( ⅰ )〜( ⅲ )より,
\(\displaystyle\frac{3-\sqrt{14}}{4}≦k≦\sqrt{14}-3\) ・・・( e )








コメント