【2022大阪公立大学・文・第1問】
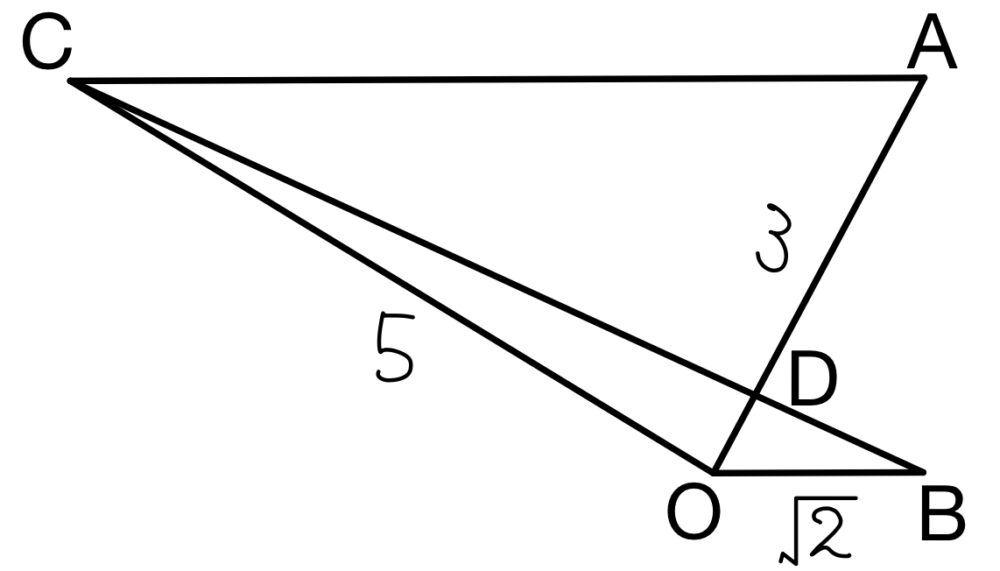
点 \(O\) を原点とする座標平面上において,点 \(A\),\(B\) が
\(\left|\overrightarrow{OA}\right|=3\),\(\left|\overrightarrow{OB}\right|=\sqrt{2}\),\(\overrightarrow{OA}\cdot\overrightarrow{OB}=2\)
を満たすとする.また,点 \(A\) を通り直線 \(OB\) と平行な直線上の点 \(C\) が
\(\left|\overrightarrow{OC}\right|=5\),\(\overrightarrow{OB}\cdot\overrightarrow{OC}<0\)
を満たすとする.直線 \(OA\) と直線 \(BC\) の交点を \(D\) とする.次の問いに答えよ.
問1 \(\overrightarrow{OC}\) を \(\overrightarrow{OA}\) と \(\overrightarrow{OB}\) を用いて表せ.
問2 \(\cos \angle AOC\) を求めよ.
問3 \(\triangle OAC\) の面積を求めよ.
問4 \(\triangle OBD\) の面積を求めよ.
解答・解説
問1 \(\overrightarrow{OC}\) を \(\overrightarrow{OA}\) と \(\overrightarrow{OB}\) を用いて表せ.
\(OB\) \(//\) \(AC\) より実数 \(t\) を用いて
\(\overrightarrow{AC}=t\overrightarrow{OB}\) とおける.
よって,\(\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{AC}=\overrightarrow{OA}+t\overrightarrow{OB}\)
\(\left|\overrightarrow{OC}\right|=5\) より \(\left|\overrightarrow{OC}\right|^2=25\)
\(\left|\overrightarrow{OA}+t\overrightarrow{OB}\right|^2=25\)
\(\left|\overrightarrow{OA}\right|^2+2t\overrightarrow{OA}\cdot\overrightarrow{OB}+t^2\left|\overrightarrow{OB}\right|^2=25\)
\(9+4t+2t^2=25\)
\(t^2+2t-8=0\)
\((t+4)(t-2)=0\)
\(t=-4,2\)
ここで \(\overrightarrow{OB}\cdot\overrightarrow{OC}<0\) より
\(\overrightarrow{OB}\cdot\left(\overrightarrow{OA}+t\overrightarrow{OB}\right)=\overrightarrow{OA}\cdot\overrightarrow{OB}+t\left|\overrightarrow{OB}\right|^2<0\)
\(2+2t<0\)
\(t<-1\) であるから,\(t=-4\)
したがって,\(\overrightarrow{OC}=\overrightarrow{OA}-4\overrightarrow{OB}\)
問2 \(\cos \angle AOC\)
\(\overrightarrow{OA}\cdot\overrightarrow{OC}=\overrightarrow{OA}\cdot\left(\overrightarrow{OA}-4\overrightarrow{OB}\right)=\left|\overrightarrow{OA}\right|^2-4\overrightarrow{OA}\cdot\overrightarrow{OB}\) より
\(\overrightarrow{OA}\cdot\overrightarrow{OC}=9-4\times 2=1\)
\(\cos\angle AOC=\displaystyle\frac{\overrightarrow{OA}\cdot\overrightarrow{OC}}{\left|\overrightarrow{OA}\right|\left|\overrightarrow{OC}\right|}=\displaystyle\frac{1}{15}\)
問3 \(\triangle OAC\) の面積
【重要公式】三角形の面積公式(ベクトル)
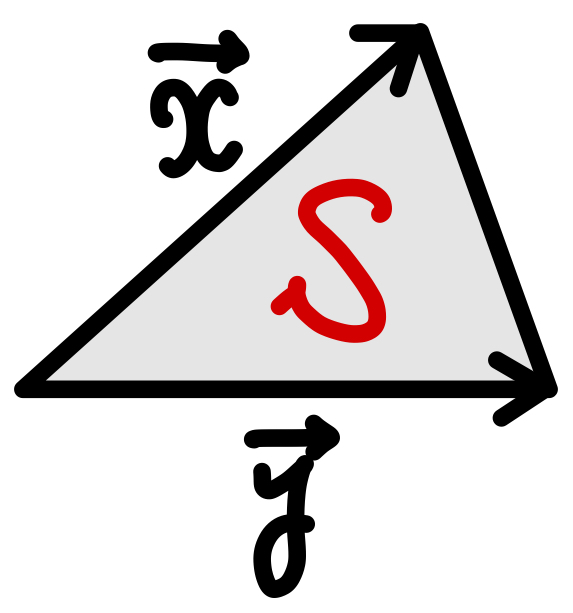 【重要公式】三角形の面積公式(ベクトル)
【重要公式】三角形の面積公式(ベクトル)
\(S=\displaystyle\frac{1}{2}\sqrt{\left|\overrightarrow{x}\right|^2\left|\overrightarrow{y}\right|^2-\left(\overrightarrow{x}\cdot\overrightarrow{y}\right)^2}\)
\(\triangle AOC=\displaystyle\frac{1}{2}\sqrt{\left|\overrightarrow{OA}\right|^2\left|\overrightarrow{OC}\right|^2-\left(\overrightarrow{OA}\cdot\overrightarrow{OC}\right)^2}\) より
\(\triangle AOC=\displaystyle\frac{1}{2}\sqrt{9\times 25-1}=2\sqrt{14}\)

問2でコサインの値を求めたので,サインの値を求めてから面積を求めてもOKです!
ただ上の面積公式は最重要公式の1つになりますので,しっかりと使えるように!
問4 \(\triangle OBD\) の面積

\(\triangle OBD\) と \(\triangle ACD\) は相似な三角形であり,また問1から \(\overrightarrow{AC}=-\overrightarrow{OB}\) より,
\(OB:AC=1:4\)
よって相似比は \(OD:AD=1:4\)
ゆえに面積比は \(\triangle OBD:\triangle ACD=1:16\)
\(\triangle OBD=\displaystyle\frac{1}{16}\triangle ACD\) ・・・①
また,\(\triangle ACD=\displaystyle\frac{AD}{OA}\triangle OAC=\displaystyle\frac{4}{5}\times 2\sqrt{14}=\displaystyle\frac{8\sqrt{14}}{5}\)
①より,\(\triangle OBD=\displaystyle\frac{1}{16}\times \displaystyle\frac{8\sqrt{14}}{5}=\displaystyle\frac{\sqrt{14}}{10}\)






コメント