【2022昭和大学・薬・歯(一部)】
\(3\) 点 \(A(3,0,0)\)，\(B(0,1,0)\)，\(C(0,0,2)\) の定める平面を \(\alpha\) とし，原点 \(O\) から平面 \(\alpha\) に垂線 \(OH\) を下ろす．垂線 \(OH\) の長さを求めよ．
考え方(平面の方程式について)
本問では，四面体 \(OABC\) の体積に注目して，
① \(\triangle OAB\) を底面，\(OC\) を高さ
② \(\triangle ABC\) を底面，\(OH\) を高さ
と \(2\) 通りで考えて処理すれば求めることができる典型・頻出問題ですね！
ただここでは，この解法ではなく，「平面の方程式，点と面の距離の公式」を利用した解法を紹介！難関大学では頻出の考え方になりますので，この問題で演習を！
平面の方程式
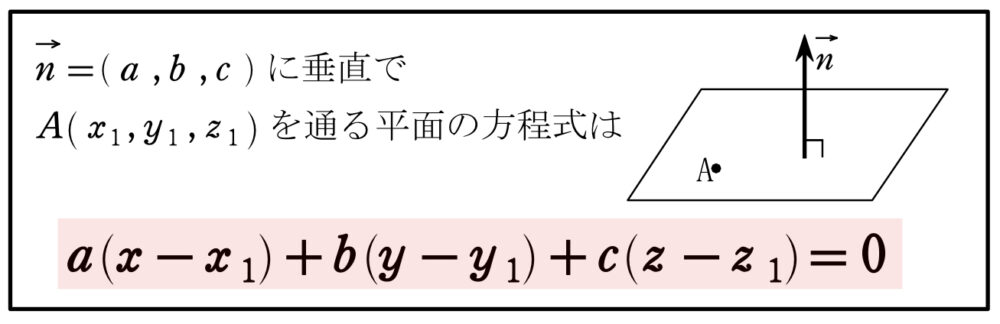
公式の証明や使い方などについては、「平面の方程式・点と平面の距離・空間上の直線の方程式・外積の公式まとめ・例題演習」を参考にしてください！
参考（\(x\)切片，\(y\)切片，\(z\)切片を通る平面の方程式）
本問では \(A(3,0,0)\) , \(B(0,1,0)\) , \(C(0,0,2)\) を通る平面 \(ABC\) の方程式だからすぐに求められますね！
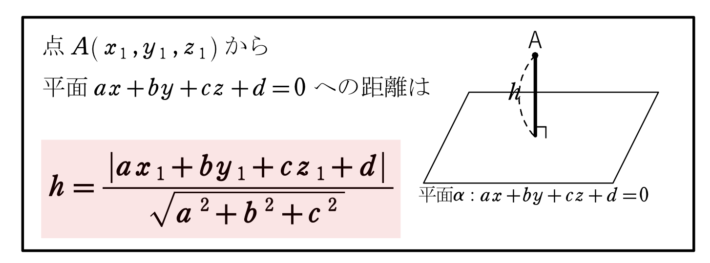
点と平面の距離の公式・証明
【2021京都大学(理)】平面に対称な点｜平面の方程式の利用｜数学B空間ベクトル
平面の方程式と平面に関して対称な点。平面の方程式は学校ではあまり学習しないが入試頻出の差がつくテーマ。数学B空間ベクトル。京大過去問演習。２次試験対策。頻出・重要問題。外積、平面の方程式の利用。
mathmathmanabu.com
2022.06.05
【2022九州大学】平面に対称な点｜外積・平面の方程式・点と面の距離の公式｜差がつく良問
学校では学習しないが入試頻出の差がつくテーマ。数学B空間ベクトル。２次試験対策。平面の方程式と平面に関して対称な点。頻出・重要問題。外積、平面の方程式、点と面の距離の公式の利用。
mathmathmanabu.com
2022.05.28
解答・解説
平面 \(\alpha\) の方程式は
\(\displaystyle\frac{x}{3}+y+\displaystyle\frac{z}{2}=1\)
\(\iff\) \(2x+6y+3z-6=0\)
原点 \(O\) から平面 \(\alpha\) までの距離は
\(OH=\displaystyle\frac{|2\cdot 0+6\cdot 0+3\cdot 0-6|}{\sqrt{2^2+6^2+3^2}}=\displaystyle\frac{6}{7}\)
コメント