【2023大阪大学・文系・第3問】
平面上の \(3\) 点 \(O\) , \(A\) , \(B\) が
\(\left|2\overrightarrow{OA}+\overrightarrow{OB}\right|=\left|\overrightarrow{OA}+2\overrightarrow{OB}\right|=1\) かつ \(\left(2\overrightarrow{OA}+\overrightarrow{OB}\right)\cdot\left(\overrightarrow{OA}+\overrightarrow{OB}\right)=\displaystyle\frac{1}{3}\)
をみたすとする.
(1) \(\left(2\overrightarrow{OA}+\overrightarrow{OB}\right)\cdot\left(\overrightarrow{OA}+2\overrightarrow{OB}\right)\) を求めよ.
(2) 平面上の点 \(P\) が
\(\left|\overrightarrow{OP}-\left(\overrightarrow{OA}+\overrightarrow{OB}\right)\right|≦\displaystyle\frac{1}{3}\) かつ \(\overrightarrow{OP}\cdot\left(2\overrightarrow{OA}+\overrightarrow{OB}\right)≦\displaystyle\frac{1}{3}\)
をみたすように動くとき,\(\left|\overrightarrow{OP}\right|\) の最大値と最小値を求めよ.
解答・解説
(1)
\(\left|2\overrightarrow{OA}+\overrightarrow{OB}\right|=\left|\overrightarrow{OA}+2\overrightarrow{OB}\right|=1\) ・・・①
\(\left(2\overrightarrow{OA}+\overrightarrow{OB}\right)\cdot\left(\overrightarrow{OA}+\overrightarrow{OB}\right)=\displaystyle\frac{1}{3}\) ・・・②
\(2\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{x}\) ・・・③
\(\overrightarrow{OA}+2\overrightarrow{OB}=\overrightarrow{y}\) ・・・④
とおく.
①,③,④より \(\left|\overrightarrow{x}\right|=\left|\overrightarrow{y}\right|=1\) ・・・⑤
③+④より
\(3\left(\overrightarrow{OA}+\overrightarrow{OB}\right)=\overrightarrow{x}+\overrightarrow{y}\)
よって,\(\overrightarrow{OA}+\overrightarrow{OB}=\displaystyle\frac{1}{3}\left(\overrightarrow{x}+\overrightarrow{y}\right)\) ・・・⑥
②,③,⑥より
\(\overrightarrow{x}\cdot\displaystyle\frac{1}{3}\left(\overrightarrow{x}+\overrightarrow{y}\right)=\displaystyle\frac{1}{3}\)
よって,\(\left|\overrightarrow{x}\right|^2+\overrightarrow{x}\cdot\overrightarrow{y}=1\)
⑤より \(\overrightarrow{x}\cdot\overrightarrow{y}=0\) ・・・⑦
したがって, \(\left(2\overrightarrow{OA}+\overrightarrow{OB}\right)\cdot\left(\overrightarrow{OA}+2\overrightarrow{OB}\right)=0\)
(2)
⑤,⑦より
\(\overrightarrow{x}=(1,0)\),\(\overrightarrow{y}=(0,1)\) とすると
\(\left|\overrightarrow{OP}-\left(\overrightarrow{OA}+\overrightarrow{OB}\right)\right|≦\displaystyle\frac{1}{3}\) より
点 \(P\) は中心 \(\displaystyle\frac{1}{3}\left(\overrightarrow{x}+\overrightarrow{y}\right)=\left(\displaystyle\frac{1}{3},\displaystyle\frac{1}{3}\right)\) ,半径 \(\displaystyle\frac{1}{3}\) の円の周および内部を表す.
また \(\overrightarrow{OP}\cdot\left(2\overrightarrow{OA}+\overrightarrow{OB}\right)≦\displaystyle\frac{1}{3}\) より
\(P(x,y\) とすると,\(x≦\displaystyle\frac{1}{3}\)
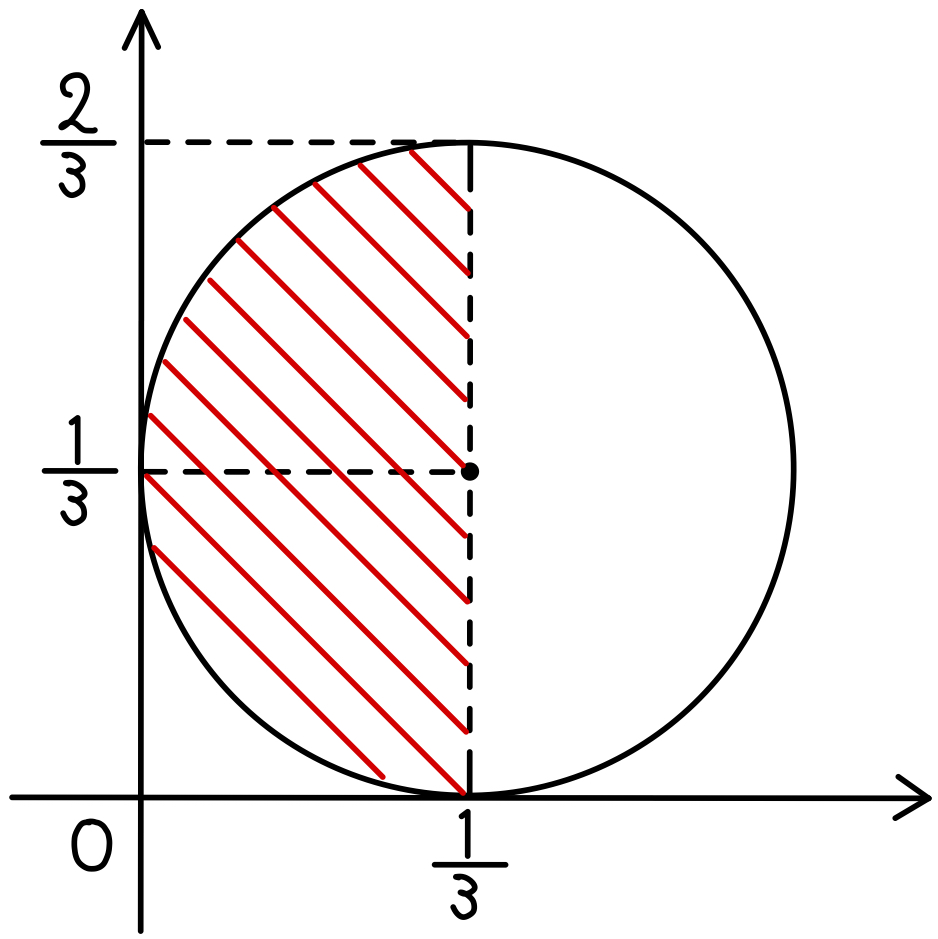 したがって点 \(P\) が動く範囲は
したがって点 \(P\) が動く範囲は
右図の斜線部分(境界線を含む)
\(\left|\overrightarrow{OP}\right|\) の最大値は \(P\left(\displaystyle\frac{1}{3},\displaystyle\frac{2}{3}\right)\) のとき
\(\left|\overrightarrow{OP}\right|=\sqrt{\left(\displaystyle\frac{1}{3}\right)^2+\left(\displaystyle\frac{2}{3}\right)^2}=\displaystyle\frac{\sqrt{5}}{3}\)
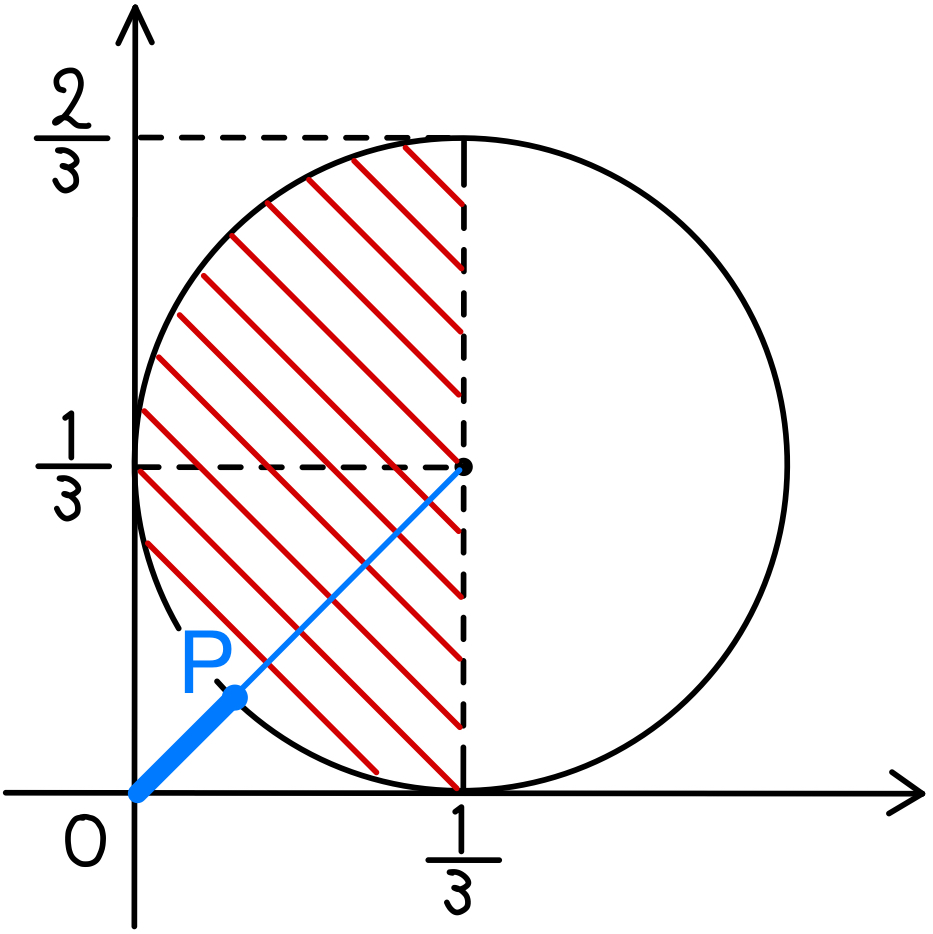
\(\left|\overrightarrow{OP}\right|\) の最小値は
右図のように
原点と円の中心を通る線分と,円の交点が \(P\) のとき
よって最小値は \(\displaystyle\frac{\sqrt{2}}{3}-\displaystyle\frac{1}{3}\)







コメント