【2023神戸大学・文科系・第1問】
\(a\),\(b\) を実数とする.整式 \(f(x)\) を \(f(x)=x^2+ax+b\) で定める.
以下の問に答えよ.
(1) \(2\) 次方程式 \(f(x)=0\) が異なる \(2\) つの正の解をもつための \(a\) と \(b\) がみたすべき必要十分条件を求めよ.
(2) \(2\) 次方程式 \(f(x)=0\) が異なる \(2\) つの実数解をもち,それらが共に \(-1\) より大きく,\(0\) より小さくなるような点 \((a,b)\) の存在する範囲を \(ab\) 平面上に図示せよ.
(3) \(2\) 次方程式 \(f(x)=0\) の \(2\) つの解の実部が共に \(-1\) より大きく,\(0\) より小さくなるような点 \((a,b)\) の存在する範囲を \(ab\) 平面上に図示せよ.ただし,\(2\) 次方程式の重解は \(2\) つと数える.
解の配置
\(2\) 次方程式が○○の範囲に実数解を持つ
⇒ 解の配置(分離)の問題

ただ実数解を持つだけでなく、ある範囲に解を持つという問題です!
\(2\) 次関数の問題においては,『最大・最小値の問題』と『解の配置』の問題は頻出ですので,しっかりとマスターしましょう!

解答・解説
(1) 異なる \(2\) つの正の解をもつための条件
\(f(x)=x^2+ax+b\) より
\(f(x)=\left(x+\displaystyle\frac{a}{2}\right)^2-\displaystyle\frac{a^2}{4}+b\)
\(y=f(x)\) の軸は \(x=-\displaystyle\frac{a}{2}\)
\(f(x)=0\) の判別式を \(D\) とすると \(D=a^2-4b\)
\(f(x)=0\) が異なる \(2\) つの正の解をもつとき
\(\begin{cases}D>0\\-\displaystyle\frac{a}{2}>0\\f(0)>0\end{cases}\) \(\iff\) \(\begin{cases}b<\displaystyle\frac{1}{4}a^2\\a<0\\b>0\end{cases}\)
(2) \(-1\) より大きく\(0\) より小さい異なる \(2\) つの実数解をもつ条件
\(f(x)=0\) が異なる \(2\) つの実数解をもち,それらが共に \(-1\) より大きく,\(0\) より小さくなるとき
\(\begin{cases}D>0\\-1<-\displaystyle\frac{a}{2}<0\\f(-1)>0\\f(0)>0\end{cases}\) \(\iff\) \(\begin{cases}b<\displaystyle\frac{1}{4}a^2\\0<a<2\\b>a-1\\b>0\end{cases}\)
よって求める範囲は下図の斜線部分(ただし境界線上を含まない)
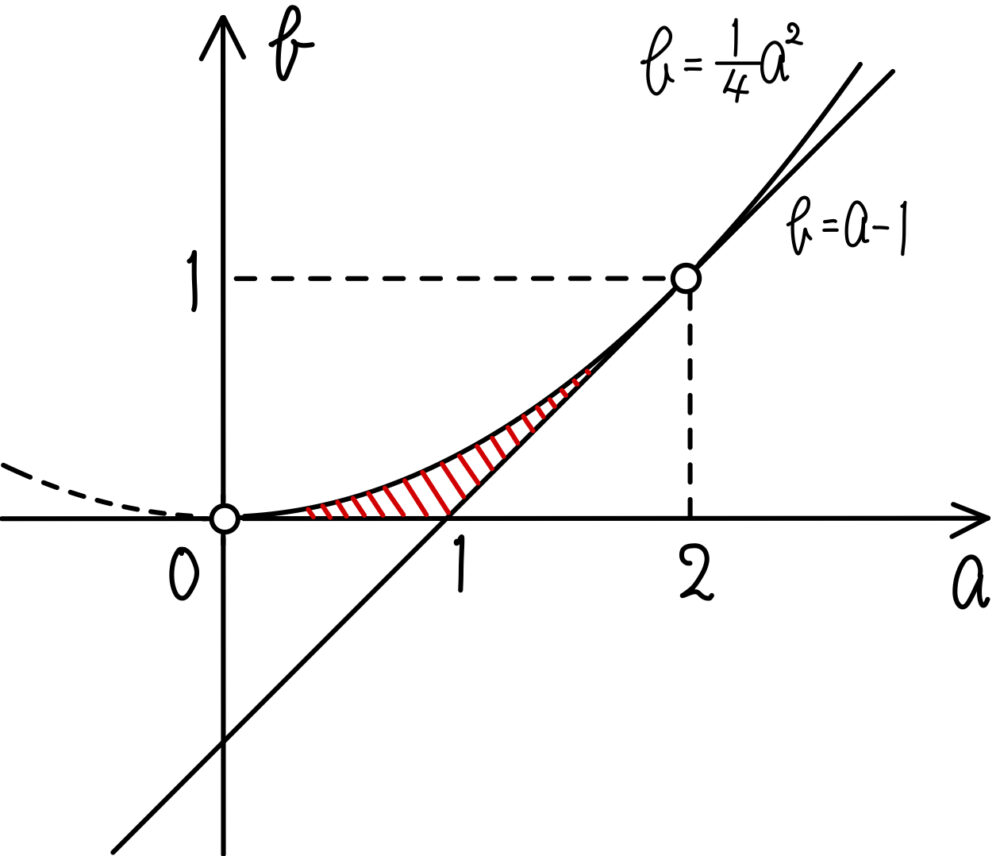

\(b=\displaystyle\frac{1}{4}a^2\) と \(b=a-1\) について
\(\displaystyle\frac{1}{4}a^2=a-1\) \(\iff\) \(a^2-4a+4=0\)
\(\iff\) \((a-2)^2=0\) となり,\(a=2\) で重解をもちます。
つまり, \(b=\displaystyle\frac{1}{4}a^2\) と \(b=a-1\) のグラフを図示する際は,必ず接するようなグラフを図示しましょう!
(3) \(2\) つの解の実部が共に \(-1\) より大きく\(0\) より小さくなる条件
( ⅰ ) \(f(x)=0\) が実数解をもつとき
(2)と同様に考え
\(\begin{cases}D≧0\\-1<-\displaystyle\frac{a}{2}<0\\f(-1)>0\\f(0)>0\end{cases}\) \(\iff\) \(\begin{cases}b≦\displaystyle\frac{1}{4}a^2\\0<a<2\\b>a-1\\b>0\end{cases}\)
( ⅱ ) \(f(x)=0\) が虚数解をもつとき
\(D<0\) のとき
\(f(x)=0\) を解くと
\(x=\displaystyle\frac{-a\pm\sqrt{D}}{2}=-\displaystyle\frac{a}{2}\pm\displaystyle\frac{\sqrt{-D}}{2}i\) より
題意を満たすのは
\(\begin{cases}D<0\\-1<-\displaystyle\frac{a}{2}<0 \end{cases}\) \(\iff\) \(\begin{cases}b>\displaystyle\frac{1}{4}a^2\\0<a<2\end{cases}\)
( ⅰ ),( ⅱ )より求める範囲は下図の斜線部分(ただし境界線上を含まない)
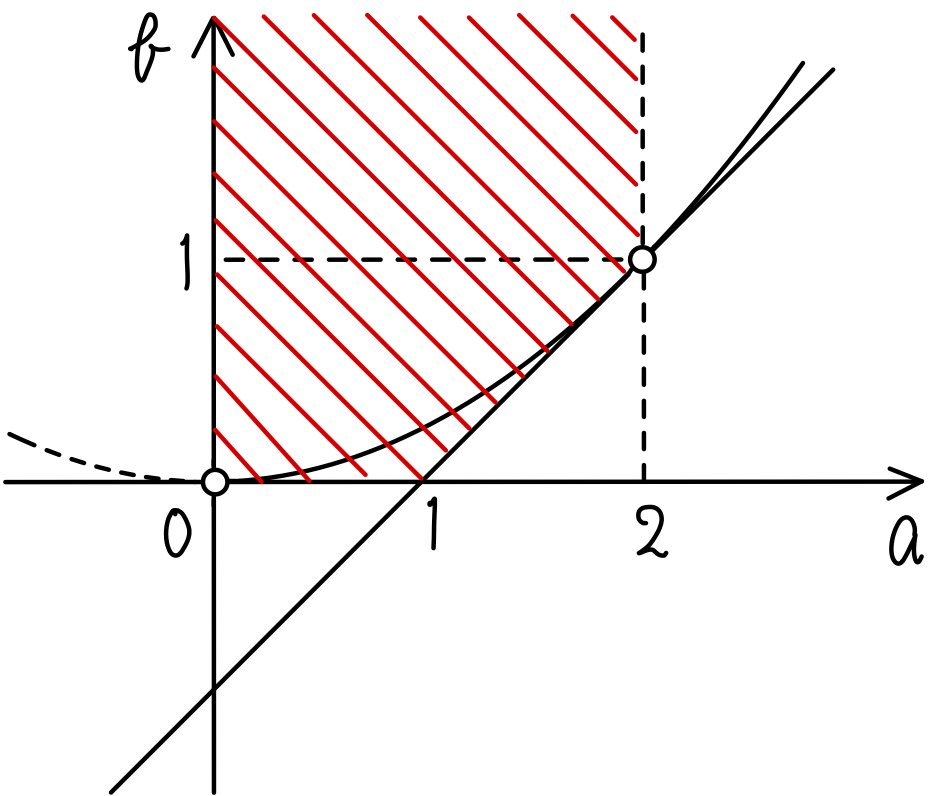








コメント