【2023一橋大学・第4問】
\(xy\) 平面上で,\(x\) 座標と \(y\) 座標がともに正の整数であるような各点に,下の図のような番号をつける.点 \((m,n)\) につけた番号を \(f(m,n)\) とする.たとえば,\(f(1,1)=1\),\(f(3,4)=19\) である.
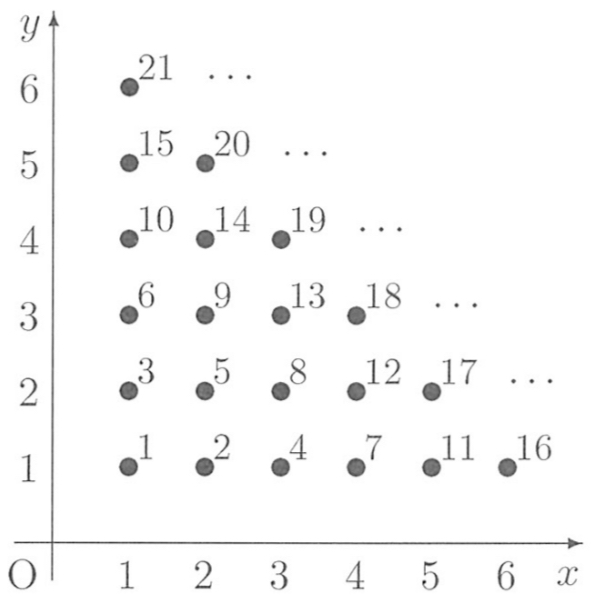
(1) \(f(m,n)+f(m+1,n+1)=2f(m,n+1)\) が成り立つことを示せ.
(2) \(f(m,n)+f(m+1,n)+f(m,n+1)+f(m+1,n+1)=2023\) となるような整数の組 \((m,n)\) を求めよ.
解答・解説
(1) \(f(m,n)+f(m+1,n+1)=2f(m,n+1)\) が成り立つことを示せ.
第 \(1\) 群:\((1,1)\)
第 \(2\) 群:\((2,1),(1,2)\)
第 \(3\) 群:\((3,1),(2,2),(1,3)\)
\(\cdots\)
第 \(k\) 群:\((k,1),(k-1,2),\cdots,(1,k)\)
とおく.
第 \(k\) 群には \(k\) 個ずつの要素があるので
\(m≧2\) のとき
第 \(m\) 群の初項 \((m,1)\) は第 \(1\) 群の初項から数えて
\(\left\{1+2+\cdots+(m-1)\right\}+1=\displaystyle\sum_{k=1}^{m-1}{k}+1=\displaystyle\frac{1}{2}m(m-1)+1\) 番目
これは \(m=1\) のときも成立.
よって,\(f(m,1)=\displaystyle\frac{1}{2}m(m-1)+1\)
点 \((m,n)\) は第 \((m+n-1)\) 群の第 \(n\) 項より
\(f(m,n)=f(m+n-1,1)+n-1\)
\(=\displaystyle\frac{1}{2}(m+n-1)(m+n-2)+1+n-1\)
\(=\displaystyle\frac{1}{2}(m+n)^2-\displaystyle\frac{3}{2}(m+n)+n+1\) ・・・①
また,点 \((m+1,n+1)\) は第 \((m+n+1)\) 群の第 \(n+1\) 項より
\(f(m+1,n+1)=f(m+n+1,1)+n\)
\(=\displaystyle\frac{1}{2}(m+n+1)(m+n)+1+n\)
\(=\displaystyle\frac{1}{2}(m+n)^2+\displaystyle\frac{1}{2}(m+n)+n+1\) ・・・②
さらに,点 \((m,n+1)\) は第 \((m+n)\) 群の第 \(n+1\) 項より
\(f(m,n+1)=f(m+n,1)+n\)
\(=\displaystyle\frac{1}{2}(m+n)(m+n-1)+1+n\)
\(=\displaystyle\frac{1}{2}(m+n)^2-\displaystyle\frac{1}{2}(m+n)+n+1\) ・・・③
①〜③より
\(f(m,n)+f(m+1,n+1)\)
\(=\displaystyle\frac{1}{2}(m+n)^2-\displaystyle\frac{3}{2}(m+n)+n+1+\displaystyle\frac{1}{2}(m+n)^2+\displaystyle\frac{1}{2}(m+n)+n+1\)
\(=(m+n)^2-(m+n)+2(n+1)\)
\(=2f(m,n+1)\)
(2) \(f(m,n)+f(m+1,n)+f(m,n+1)+f(m+1,n+1)=2023\) となるような整数の組
点 \((m+1,n)\) は第 \((m+n)\) 群の第 \(n\) 項より
\(f(m+1,n)=f(m+n,1)+(n-1)\)
\(=\displaystyle\frac{1}{2}(m+n)(m+n-1)+1+n-1\)
\(=\displaystyle\frac{1}{2}(m+n)^2-\displaystyle\frac{1}{2}(m+n)+n\) ・・・④
(1)の結果より
\(f(m,n)+f(m+1,n)+f(m,n+1)+f(m+1,n+1)=2023\)
\(\iff\) \(f(m+1,n)+3f(m,n+1)=2023\)
③,④より
\(\displaystyle\frac{1}{2}(m+n)^2-\displaystyle\frac{1}{2}(m+n)+n+3\left\{\displaystyle\frac{1}{2}(m+n)^2-\displaystyle\frac{1}{2}(m+n)+n+1\right\}=2023\)
\(2(m+n)^2-2(m+n)+4n+3=2023\)
\((m+n-1)(m+n)=1010-2n\)
\((m+n-1)(m+n)\) は連続する \(2\) つの整数の積であり,
右辺の \(1010-2n\) は単調に減少することに注目すると

\(31\times 32=992\),\(32\times 33=1056\) となるので
\(m+n=32\) 近辺で吟味すればよいことがわかりますね!
( ⅰ ) \(m+n≧33\) のとき
\((m+n-1)(m+n)≧32\times 33=1056>1010-2n\) より
題意を満たす整数の組 \((m,n)\) は存在しない.
( ⅱ ) \(m+n=32\) のとき
\((m+n-1)(m+n)=1010-2n\)
\(\iff\) \(31\times 32=1010-2n\)
よって \(n=9\)
ゆえに,\((m,n)=(23,9)\)
( ⅲ ) \(m+n≦31\) のとき
\((m+n-1)(m+n)≦30\times 31=930\),
\(1010-2n≧1010-2\times 30=950\) より
題意を満たす整数の組 \((m,n)\) は存在しない.
したがって,求める整数の組 \((m,n)=(23,9)\)








コメント