【入試問題】
(1) \(x>-2\) のとき
\(y=\displaystyle\frac{x^2+3x+3}{x+2}\) の最小値を求めよ.
(2) \(BC=5 , CA=7 , AB=6\) の\(△ABC\) の、辺 \(AB\) 上に点 \(D\) を、辺 \(AC\) 上に点 \(E\) をとり、 \(△ADE\) の面積が \(△ABC\) の面積の \(\displaystyle\frac{1}{3}\) となるようにする.\(DE\) の長さの最小値を求めよ.
![]()
はじめに
今回のテーマである「相加平均・相乗平均の関係」は受験数学において頻出であり、最重要テーマの 1 つです.そして「相加平均・相乗平均の関係」に関しては、分野を問わず出題されることが多いため、ただ公式を覚えているだけでは使い物になりません.
「いつ・どのタイミングで使うのか」が非常に重要になります.
基本的な問題で相加平均・相乗平均の確認をしたい場合は、
相加平均・相乗平均の関係はいつ使う?使うタイミングの見抜き方(基本)
を確認してください.
相加平均・相乗平均の関係
【相加平均・相乗平均の関係】
\(A≧0 , B≧0\) のとき
\(A+B≧2\sqrt{AB}\)
等号成立は、\(A=B\) のとき
相加平均・相乗平均を使うタイミング
次の2つの形を見たら相加平均・相乗平均の関係を疑え!
1.逆数の和の形
👉 ルートの中で約分され、文字が消える!
2.和と積の形
👉\(和≧2\sqrt{積}\)
※相加平均・相乗平均の関係は 0 以上の数でしか使用できないため、「0 以上の数になるための条件」が必ず存在する
※相加平均・相乗平均の関係を使用した場合、必ず等号成立を確認するように!
☞なぜに等号成立を言う必要があるのか?
少し難しい内容になりますが、数学的に非常に重要なお話しになります。
「最大値とは?等号成立の必要性について」に簡単にまとめていますので、確認を!
和と積の形を見たら
※範囲(最大値や最小値を含む)に関する問題の時は、相加平均・相乗平均の関係を使うことが多い.
(1)考え方・解答
(1) \(x>-2\) のとき
\(y=\displaystyle\frac{x^2+3x+3}{x+2}\) の最小値を求めよ.
(分母の次数)≦(分子の次数)
👉 割り算(次数下げ)
※このPointは、分数関数を扱う際によくやる手段です!
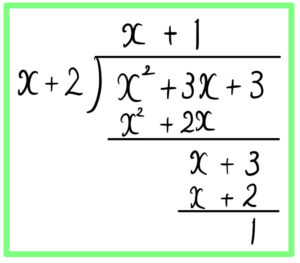
\(x^2+3x+3=(x+1)(x+2)+1\) より
\(\displaystyle\frac{x^2+3x+3}{x+2}=\displaystyle\frac{(x+1)(x+2)+1}{x+2}\)
よって
\(y=x+1+\displaystyle\frac{1}{x+2}\) ・・・①

理想!!
\(y=x+1+\displaystyle\frac{1}{x+1}\)
または
\(y=x+2+\displaystyle\frac{1}{x+2}\)
だったら「逆数の和の形」になるため、
相加平均・相乗平均の関係が使用できる.
①を前者の形に変形することは・・・
ただ①を後者の形に変形しようと思えば、
\(y=(x+2)+\displaystyle\frac{1}{x+2}-1\)
と理想的な形と現実のギャップを埋めるための調整を行った!
\(x>-2\) より \(x+2>0\) なので、相加平均・相乗平均の関係から
\((x+2)+\displaystyle\frac{1}{x+2}≧2\sqrt{(x+2)\times \displaystyle\frac{1}{x+2}}=2\)
両辺から 1 を引くと、
\(y≧1\)
等号成立は、
\((x+2)=\displaystyle\frac{1}{x+2}\)
\((x+2)^2=1\)
\(x+2>0\) より
\(x+2=1\)
\(x=-1\) のとき、\(y\) の最小値は 1
(2)考え方・解答
\(AD=x , AE=y\) とおく.(\(0<x<6 , 0<y<7\))
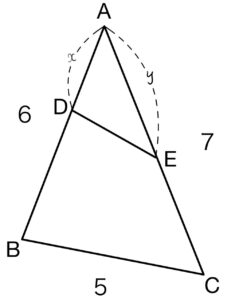
\(△ABC=\displaystyle\frac{1}{2}\times 6\times 7 \times sinA=21sinA\)
\(△ADE=\displaystyle\frac{1}{2}xysinA\) であり、
\(△ADE=\displaystyle\frac{1}{3}△ABC \) より
\(xy=14\) ・・・①
\(△ABC\) で余弦定理より、
\(cosA=\displaystyle\frac{6^2+7^2-5^2}{2\cdot 6\cdot 7}=\displaystyle\frac{5}{7}\) ・・・②
また、\(△ADE\) で余弦定理より、
\(DE^2=x^2+y^2-2xycosA\)
①、②より
\(DE^2=x^2+y^2-20\) ・・・③

① ☞ 積の形
③ ☞ \(x^2+y^2\) 和の形
があり、さらに最小値を問われていることから、
相加平均・相乗平均の関係を疑う!
\(x>0 , y>0\) より相加平均・相乗平均の関係から、
\(x^2+y^2≧2\sqrt{x^2y^2}=2xy=28\)
\(x^2+y^2-20≧28-20=8\)
\(DE^2≧8\)
\(DE≧2\sqrt{2}\)
等号成立は、
\(x^2=y^2\) かつ ① より
\(x=y=\sqrt{14}\) のとき、\(DE\) の最小値は\(2\sqrt{2}\)










コメント