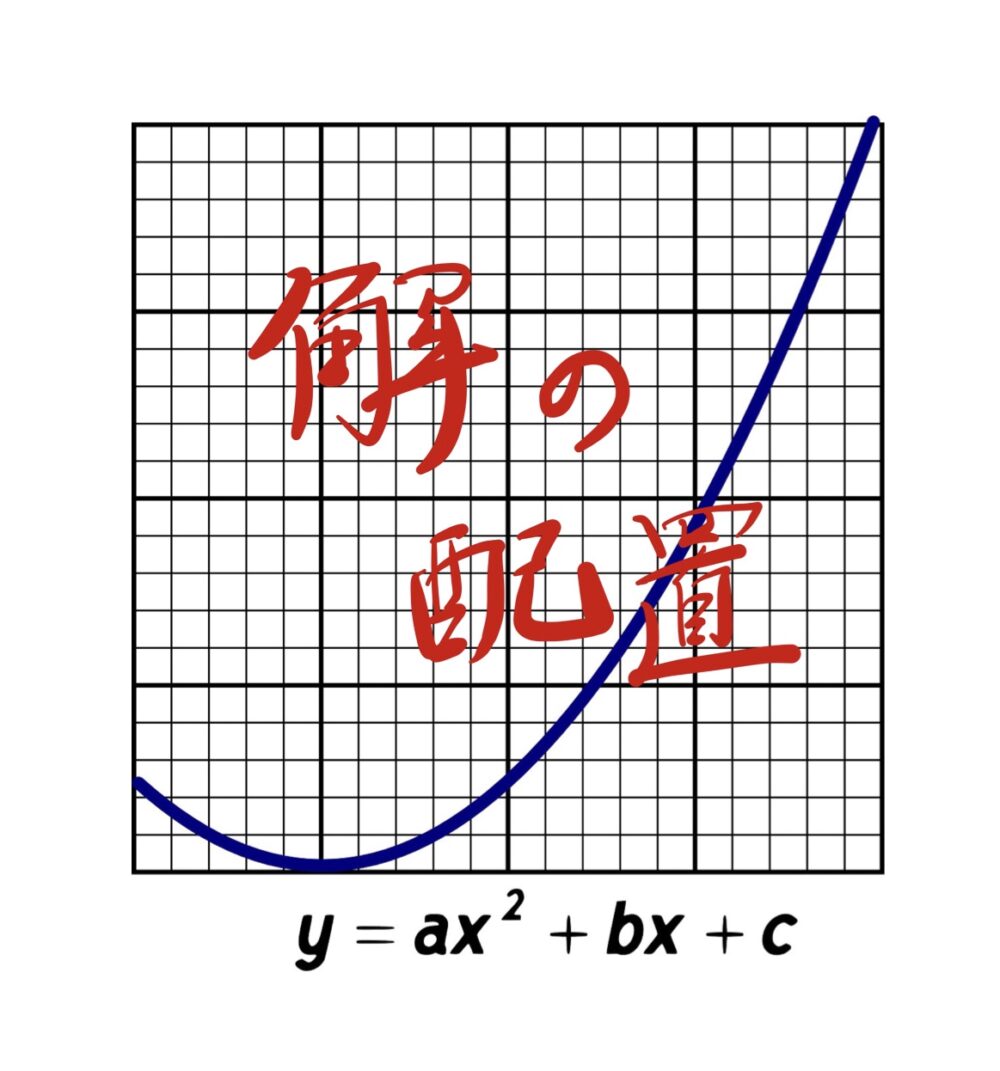
 2次関数
2次関数 【頻出】2次関数の解の配置(分離):1より大きい異なる2つの解、異符号の解など2パターン完全マスター
2次関数で絶対におさえたい2テーマのうちの1つ。ただ解を持つだけでなく「ある範囲に解をもつ」タイプの問題(解の配置)を完全マスター。例:正の異なる2つの実数解。1より大きい異なる2つの解。異符号の解など。定期テストや入試では頻出テーマになります。解法2パターン。
 2次関数
2次関数 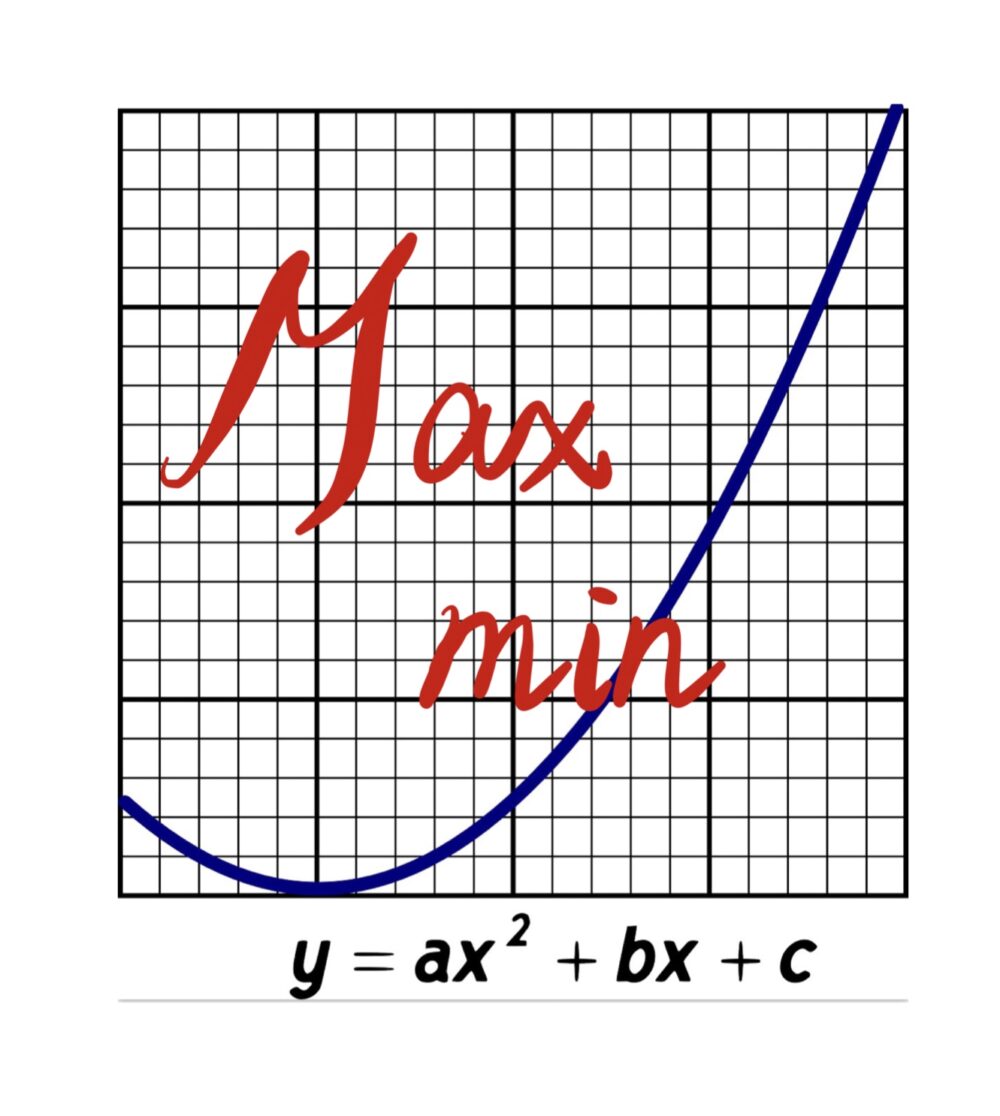 2次関数
2次関数 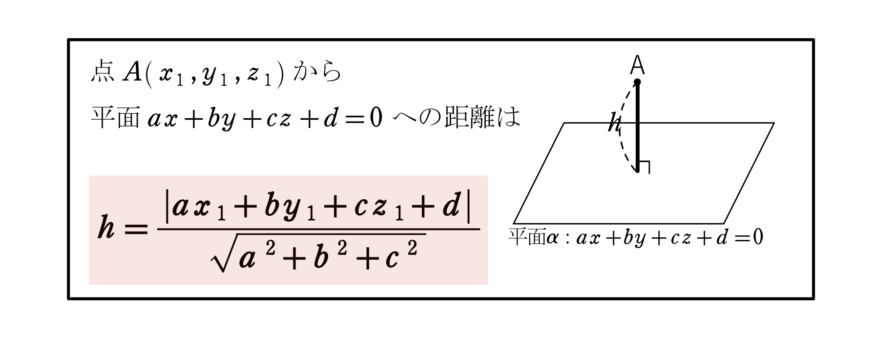 ベクトル
ベクトル  場合の数・確率
場合の数・確率  大学受験情報
大学受験情報 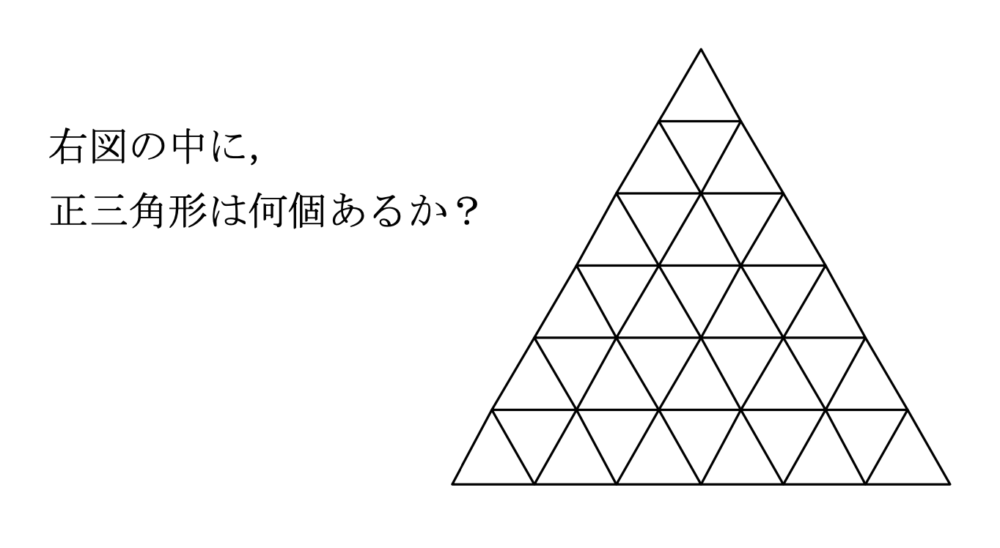 場合の数・確率
場合の数・確率  図形と方程式
図形と方程式  整数問題
整数問題  整数問題
整数問題  大学受験情報
大学受験情報  整数問題
整数問題  大学受験情報
大学受験情報  大学受験情報
大学受験情報  大学受験情報
大学受験情報  ベクトル
ベクトル  数学(大学入試問題)
数学(大学入試問題)  大学受験情報
大学受験情報  大学受験情報
大学受験情報  大学受験情報
大学受験情報 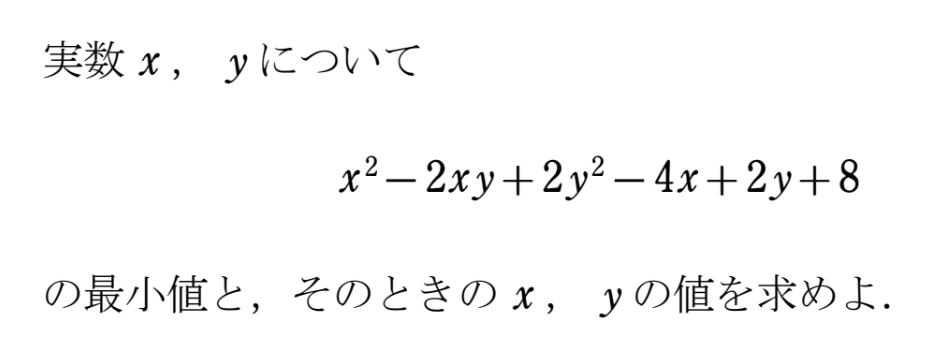 2次関数
2次関数 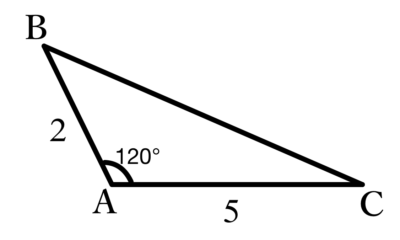 ベクトル
ベクトル  大学受験情報
大学受験情報  数学(大学入試問題)
数学(大学入試問題)