【問題】
曲線 \(y=x^3-4x\) と,その曲線上の点 \(( 1 , -3 )\) における接線で囲まれた図形の面積 \(S\) を求めよ.
接線の方程式
曲線 \(y=f(x)\) 上の点 \(A(a,f(a))\) における曲線の接線の方程式は
\(y-f(a)=f^{\prime}(a)(x-a)\)
3次関数と接線で囲まれた図形の面積
【有名】1/12 面積公式
 覚えておきたい公式!
覚えておきたい公式!
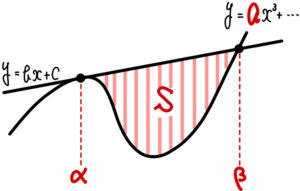
\(3\) 次関数 \(y=\)\(a\)\(x^3+\cdots\) と
その接線 \(y=bx+c\) において,
接点が \(x=\alpha\),もう一つの交点が \(x=\beta\) のとき
\(3\) 次関数とその接線で囲まれた面積 \(S\) は
\(S=\displaystyle\frac{|a|}{12}(\beta-\alpha)^4\)
公式の証明
\(3\) 次関数 \(y=ax^3+\cdots\) とその接線 \(y=bx+c\) の交点が \(x=\alpha\) ( 接点 ) と \(x=\beta\) であるから,
 \(ax^3+\cdots=bx+c\)
\(ax^3+\cdots=bx+c\)
\(\iff\) \((ax^3+\cdots)-(bx+c)=0\)
\(\iff\) \(a(x-\alpha)^2(x-\beta)=0\)
と式変形できるので
\(S=\displaystyle\int^{\beta}_{\alpha}\left\{(bx+c)-(ax^3+\cdots)\right\} dx\)
\(=\displaystyle\int^{\beta}_{\alpha}-a(x-\alpha)^2(x-\beta) dx\)

\(x-\alpha\) の形を作るために,
\(x-\beta\) を \(x\)\(-\alpha+\alpha\)\(-\beta\) として式変形!
\(=-a\displaystyle\int^{\beta}_{\alpha}(x-\alpha)^2\left\{(x-\alpha)-(\beta-\alpha)\right\} dx\)
\(=-a\displaystyle\int^{\beta}_{\alpha}\left\{(x-\alpha)^3-(\beta-\alpha)(x-\alpha)^2\right\}dx\)

\(1\) 次式の \(n\) 乗の積分
\(\displaystyle\int (ax+b)^n dx=\displaystyle\frac{1}{a(n+1)}(ax+b)^{n+1}+C\)
\(=-a\Bigl[\displaystyle\frac{1}{4}(x-\alpha)^4-\displaystyle\frac{1}{3}(\beta-\alpha)(x-\alpha)^3\Bigr]^{\beta}_{\alpha}\)
\(=-a\left\{\displaystyle\frac{1}{4}(\beta-\alpha)^4-\displaystyle\frac{1}{3}(\beta-\alpha)^4\right\}\)
\(=\displaystyle\frac{a}{12}(\beta-\alpha)^4\)

記述試験では途中過程もかけるように!
共通テスト・私大受験などマーク形式(答えのみ)でよければこの公式はしっかりと覚えておきましょう!
解答
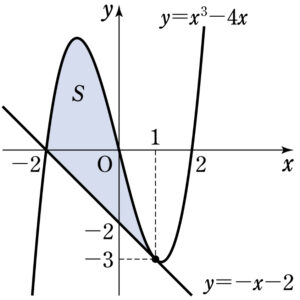
曲線 \(y=x^3-4x\) と,その曲線上の点 \(( 1 , -3 )\) における接線で囲まれた図形の面積 \(S\) を求めよ.
\(f(x)=x^3-4x\) とおく.\(f^{\prime}(x)=3x^2-4\) より
\(( 1 , -3 )\) における接線の傾きは \(f^{\prime}(1)=-1\)
よって接線の方程式は,\(y-(-3)=-(x-1)\)
つまり,\(y=-x-2\) ・・・①
\(y=f(x)\) と①の交点の \(x\) 座標は
\(x^3-4x=-x-2\)
\(x^3-3x+2=0\)

\(y=f(x)\) と① は \(x=1\) で接するので,
\((x-1)^2\) を因数にもつことに注目して因数分解をしよう!
 \((x-1)^2(x+2)=0\)
\((x-1)^2(x+2)=0\)
よって,\(x = 1 , -2\)

もう1つの交点の求め方については,変曲点の性質を利用した時短解法があります!
「【共通テスト裏技】3次関数と接線|変曲点と接点と交点について」を参考にしてください!
したがって,求める面積 \(S\) は
\(S=\displaystyle\int^{1}_{-2}\left\{(x^3-4x)-(-x-2)\right\} dx\)
\(=\displaystyle\int^{1}_{-2}(x-1)^2(x+2)dx\)

この程度の計算であれば,あとは地道に計算してもよいと思います!
しかしここでは,上で証明した形を再現しながら計算してみましょう!
※ 入試問題では計算式が文字になることが多いです。流れを覚えるために演習してみましょう!
\(S=\displaystyle\int^{1}_{-2}(x-1)^2\left\{(x-1)+3\right\}dx\)
\(=\displaystyle\int^{1}_{-2}\left\{(x-1)^3+3(x-1)^2\right\} dx\)
\(=\Bigl[\displaystyle\frac{1}{4}(x-1)^4+(x-1)^3\Bigr]^{1}_{-2}\) \(=\displaystyle\frac{27}{4}\)







コメント