【2019早稲田大学・教育】
放物線 \(y=x^2\) 上の点 \((a,a^2)\) における接線と曲線 \(y=x^3-ax\) が異なる \(3\) 点で交わるとき，\(a\) のとりうる値の範囲を求めよ．
考え方・方針の立て方について
\(f(x)=x^2\) , \(g(x)=x^3-ax\) とおく．
\(f^{\prime}(x)=2x\) より，\(y=f(x)\) 上の点 \((a,a^2)\) における接線は
\(y-a^2=2a(x-a)\)
よって，\(y=2ax-a^2\) ・・・①
①と \(y=g(x)\) が異なる \(3\) 点で交わるとき
\(x^3-ax=2ax-a^2\)
\(x^3-3ax+a^2=0\) ・・・②
②が異なる \(3\) つの実数解を持てばよい．
方程式の実数解の個数について
方程式の実数解の個数について
⇒ 適切な形に変形して，両辺のグラフの交点の個数を考える
3 次方程式の非定数分離型
②の式は，\(a= ( x\) の式 ) の形に式変形ができない・・・
このような場合はどのように考えたらよいのだろう？
※ \(a= ( x\) の式 ) の形に変形できる ⇒ 定数分離型 ( )
\(3\) 次関数のグラフの形(極大値・極小値)に注目して考えていきましょう！
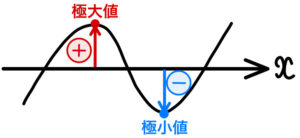②が異なる \(3\) つの実数解を持つとき，
\(y=x^3-3ax+a^2\) と \(y=0\) ( \(x\) 軸 ) と交点が異なる \(3\) つになればよいので，右図のような形になればよいね！
つまり，「極大値が正」かつ「極小値が負」の条件を満たせばよいということですか？
その条件だけでは不十分です！
これだけでは減点されてしまうので気をつけましょう！
「極大値」や「極小値」の話をするためには，「極値が存在する」ための条件を最初に記述するように！
極値が存在する条件については、「」で確認した内容ですね！
その条件において，「極大値が正」かつ「極小値が負」をそれぞれ計算すればOKですね！
極値の存在条件については忘れやすいので注意しましょう！
さらに，
「極大値が正」かつ「極小値が負」の計算については，
『(極大値)\(\times \)(極小値) \(<0\)』として計算すると，計算量が少なくなります！
\(x^3-3ax+a^2=0\) が異なる \(3\) つの実数解をもつ
\(\iff\) \(\begin{cases}y=x^3-3ax+a^2\\y=0\end{cases}\) が異なる \(3\) つの共有点をもつ
\(\rightarrow\) 次の \(2\) つの条件を満たせばよい
( ⅰ ) \(y=x^3-3ax+a^2\) が極値をもつ条件を考える
( ⅱ ) ( ⅱ ) のとき，(極大値)\(\times \)(極小値) \(<0\)
解答
\(f(x)=x^2\) , \(g(x)=x^3-ax\) とおく．
\(f^{\prime}(x)=2x\) より，\(y=f(x)\) 上の点 \((a,a^2)\) における接線は
\(y-a^2=2a(x-a)\)
よって，\(y=2ax-a^2\) ・・・①
①と \(y=g(x)\) が異なる \(3\) 点で交わるとき
\(x^3-ax=2ax-a^2\)
\(x^3-3ax+a^2=0\) ・・・②
②が異なる \(3\) つの実数解を持てばよい．
ここで，\(h(x)=x^3-3ax+a^2\) とおく．
\(3\) 次関数 \(y=h(x)\) のグラフが \(x\) 軸と異なる \(3\) つの共有点を持てばよいので，
\(h^{\prime}(x)=3x^2-3a=3(x^2-a)\)
\(h^{\prime}(x)=0\) が異なる \(2\) 実数解を持つとき，
つまり，\(a>0\) ・・・③ のとき \(y=h(x)\) のグラフは極値をもつ．
このとき，\(x=\pm\sqrt{a}\) で \(y=h(x)\) は極値をもつので
\(h(\sqrt{-a})\times h(\sqrt{a})<0\) を満たせばよい．
\((a^2+2a\sqrt{a})(a^2+2a\sqrt{a})<0\)
\(a^3(a-4)<0\)
③より \(a>0\) より，\(a-4<0\)
したがって求める条件は，\(0<a<4\)
コメント