【2021数学ⅠA(第１日程)】第５問(図形の性質)
問題と解答・解説《ア〜キ》
解答・解説《ア〜キ》
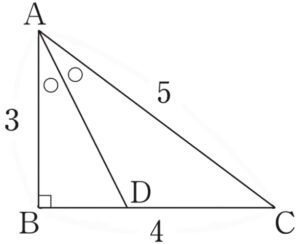
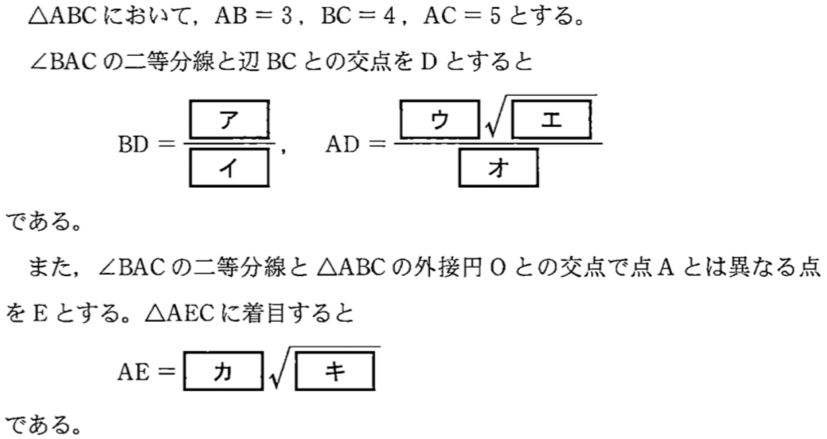
線分 \(AD\) は \(\angle BAC\) の二等分線であるから
\(BD : DC = AD : AC = 3 : 5\) より
\(BD=\displaystyle\frac{3}{3+5}\times 4=\)\(\displaystyle\frac{3}{2}\) ・・・《アイ》
また，\(AC^2=AB^2+BC^2\) より \(\triangle ABC\) は \(\angle B=90°\) の直角三角形
よって三平方の定理より
\(AD^2=AB^2+BD^2=3^2+\left(\displaystyle\frac{3}{2}\right)^2=\displaystyle\frac{45}{4}\)
したがって，\(AD=\)\(\displaystyle\frac{3\sqrt{5}}{2}\) ・・・《ウ〜オ》
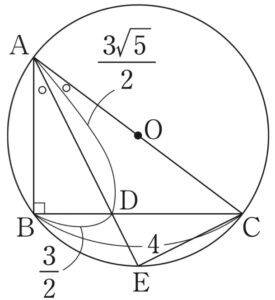\(CD=BC-BD=4-\displaystyle\frac{3}{2}=\displaystyle\frac{5}{2}\) であり，
方べきの定理より
\(AD\times DE=BD\times DC\)
\(\displaystyle\frac{3\sqrt{5}}{2}\times DE=\displaystyle\frac{3}{2}\times \displaystyle\frac{5}{2}\)
よって \(DE=\displaystyle\frac{\sqrt{5}}{2}\)
したがって，\(AE=AD+DE=\displaystyle\frac{3\sqrt{5}}{2}+\displaystyle\frac{\sqrt{5}}{2}=\)\(2\sqrt{5}\) ・・・《カキ》
問題と解答・解説《ク〜サ》
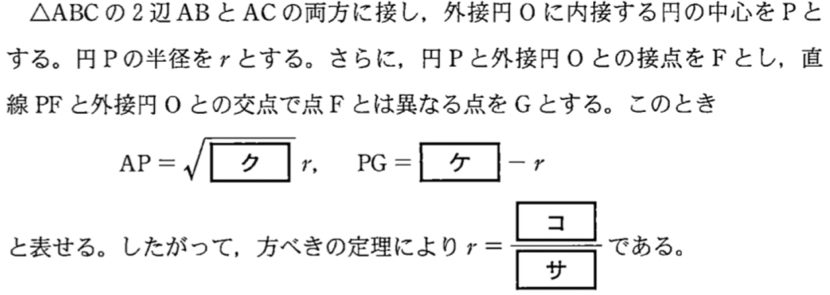
解答・解説《ク〜サ》
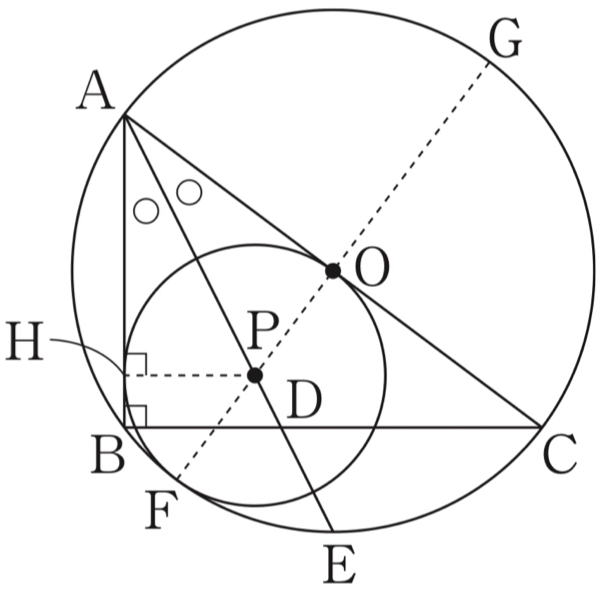
右図のように，円 \(P\) と辺 \(AB\) の接点を \(H\) とおく.
\(\triangle AHP\text{∽}\triangle ABD\) より
\(AP : AD = HP : BD\) であるから，
\(AP : \displaystyle\frac{3\sqrt{5}}{2} = r : \displaystyle\frac{3}{2}\)
よって，\(AP=\sqrt{5}r\) ・・・《ク》
また円 \(P\) と円 \(O\) の接点 \(F\) と，点 \(P\) を結ぶ直線 \(FP\) は \(2\) 円 \(P\) , \(O\) の中心どうしを結んだ直線であるから，\(FG\) は円 \(O\) の直径 \(5\) となる．
よって，\(PG=FG-FP=\)\(5-r\) ・・・《ケ》
したがって方べきの定理より，
\(AP\times PE=FP\times PG\)
\(\sqrt{5}r(2\sqrt{5}-\sqrt{5}r)=r(5-r)\)
\(r\not=0\) であるから
\(\sqrt{5}(2\sqrt{5}-\sqrt{5}r)=5-r\)
これを解くと，\(r=\displaystyle\frac{5}{4}\) ・・・《コサ》
問題と解答・解説《シ〜タ》
解答・解説《シ〜タ》
内接円の半径を \(q\) とすると，
\(\triangle ABC=\displaystyle\frac{1}{2}q(AB+BC+CA)\) より
\(\displaystyle\frac{1}{2}\times 3\times 4=\displaystyle\frac{1}{2}q(3+4+5)\)
よって，\(q=1\) ・・・《シ》
内心 \(Q\) は直線 \(AD\) 上にあるから，円 \(Q\) と辺 \(AB\) の接点を \(I\) とすると，
\(\triangle AIQ\text{∽}\triangle ABD\) より
\(AQ : AD = QI : DB\) であるから，
\(AQ : \displaystyle\frac{3\sqrt{5}}{2} = 1 : \displaystyle\frac{3}{2}\)
よって \(AQ=\sqrt{5}\) ・・・《ス》
また，\(\triangle APH\) で三平方の定理から \(AH=\displaystyle\frac{5}{2}\) ・・・《セソ》
このとき，\(AH\times AB=\displaystyle\frac{5}{2}\times 3=\displaystyle\frac{15}{2}\)
\(AQ\times AD=\sqrt{5}\times \displaystyle\frac{3\sqrt{5}}{2}=\displaystyle\frac{15}{2}\) より
\(AH\times AB=AQ\times AD\) が成り立つから，方べきの定理の逆より
\(4\) 点 \(H\) , \(B\) , \(D\) , \(Q\) は同一円周上にある．
よって点 \(H\) は \(3\) 点 \(B\) , \(D\) , \(Q\) を通る円の周上にあるので，( a ) は正しい．
次に，\(AH\times AB\not=AQ\times AE\) であるから，\(4\) 点 \(H\) , \(B\) , \(E\) , \(Q\) は同一円周上にない．よって，点 \(H\) は \(3\) 点 \(B\) , \(E\) , \(Q\) を通る円の周上にないので，( b ) は誤り．
したがって，① ・・・《タ》
コメント