\(y=\sin x\) ( \(0≦x≦\pi\) ) と \(x\) 軸とで囲まれた部分を \(y\) 軸のまわりに \(1\) 回転してできる体積を求めよ．
バームクーヘン分割について
バームクーヘン分割の公式
連続関数 \(y=f(x)\) ( \(\alpha≦x≦\beta\) ) と \(x\) 軸とで囲まれた部分を \(y\) 軸のまわりに \(1\) 回転してできる体積 \(V\) は
\(V=\displaystyle\int^{\beta}_{\alpha}2\pi x |f(x)| dx\)
バームクーヘン分割のイメージ
公式は次のイメージをしっかりと持った上で覚えましょう！
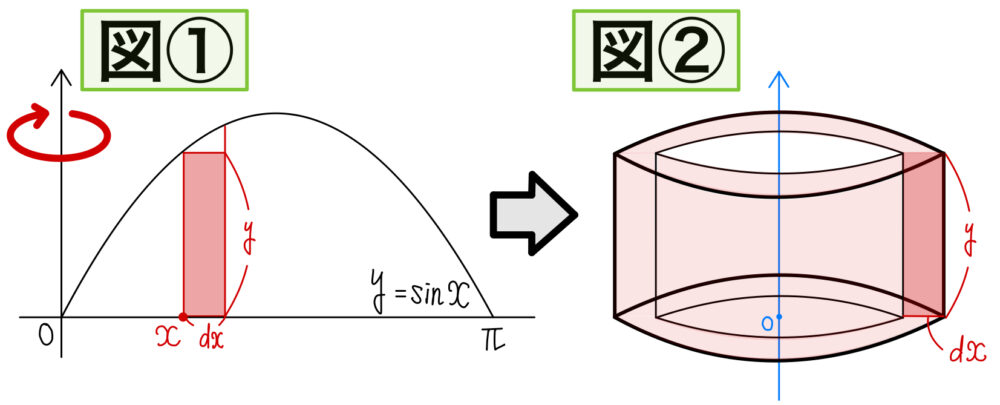
ある \(x\) のあたいにおいて，ものすごく小さい幅( \(dx\) ) をとり，図①のように長方形を考えましょう！その長方形を \(y\) 軸のまわりに回転させると，図②のような中身が切り抜かれた円柱形の体積が出来上がります。
これを \(0≦x≦\pi\) において何度も繰り返すと，バームクーヘンのように，何層にもなって最終的に求めたい体積の形が出来上がるという考え方です！
つまり，図②のバームクーヘン１層分の体積をインテグラルを使って積分すれば求めたい体積の出来上がり！
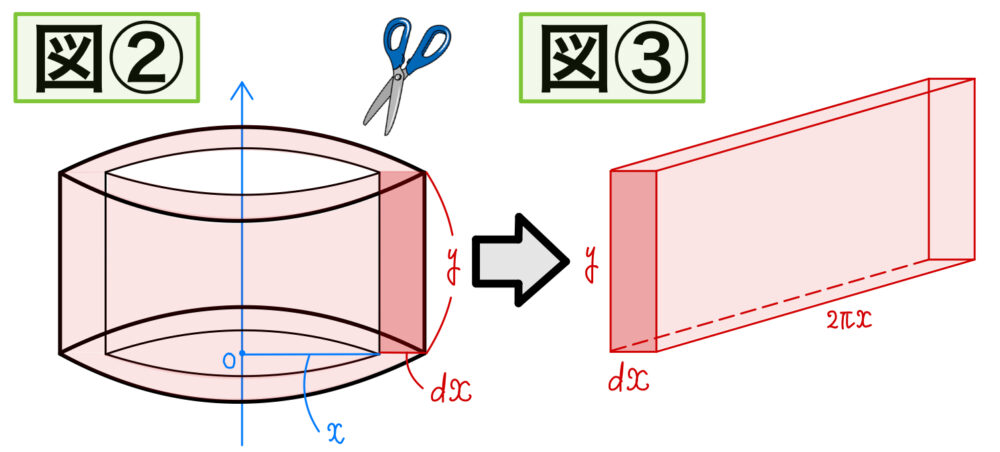
次に，図②のバームクーヘン１層分の体積について考えましょう！
チョキチョキチョキとハサミで切ると，図③のような四角柱の形になります。
(※厳密には誤差がありますが，\(dx\) はほぼほぼ “0” で考えています。あくまでもイメージですので，ここでは細かい話は一旦お許しください！)
図③の四角柱の体積は \(2\pi x\cdot y\cdot dx\) であるから，求める体積は
\(V=\displaystyle\int^{\pi}_{0}2\pi x\cdot y dx\) ということです！
解答
\(V=\displaystyle\int^{\pi}_{0}2\pi xy dx\) より
\(V=2\pi\displaystyle\int^{\pi}_{0}x\sin x dx\)
(多項式)×(三角関数)の積分ですから，部分積分が利用できますね！
公式等については，【数学Ⅲ】積分解法手順まとめ⑥(三角関数)×(多項式)の積分を確認してください。
\(V=2\pi \Bigl[-x\cos x+\sin x\Bigr]^{\pi}_{0}=2\pi^2\)
コメント