【2021名城大学】
関数 \(f(x)=x^3-3x^2+4\) を考える.\(xy\) 平面上に曲線 \(C\) : \(y=f(x)\) について,次の問に答えよ.
(1) \(C\) 上の点 \(P (p,p^3-3p^2+4)\) における接線 \(l\) の方程式を \(p\) を用いて表せ.
(2) 点 \(A(0,a)\) ( ただし,\(a\) は実数 ) を通る \(C\) の接線の本数を求めよ.
接線の方程式
曲線 \(y=f(x)\) 上の点 \(A(a,f(a))\) における曲線の接線の方程式は
\(y-f(a)=f^{\prime}(a)(x-a)\)
(1)解答
\(f(x)=x^3-3x^2+4\)
\(f^{\prime}(x)=3x^2-6x\) より,\(l\) の方程式は
\(y-(p^3-3p^2+4)=(3p^2-6p)(x-p)\)
\(y=(3p^2-6p)x-2p^3+3p^2+4\)
接線何本引けるか問題
考え方
(1)より \(y=(3p^2-6p)x-2p^3+3p^2+4\) が 点 \(A(0,a)\) を通るので,
\(a=-2p^3+3p^2+4\) ・・・①

ここから何をしたらいいの・・・?

①は \(p\) の \(3\) 次方程式となりますね!

つまり,方程式だからこれを解くと,
\(p =\)○,△,□ のように解を \(1\) 〜 \(3\) 個持つってことですね!
その解は何を意味するの??

その通りです!
そもそも \(p\) は接点の \(x\) 座標のことですから・・・

接点の個数が分かれば,接線の本数もわかる!
当然,「接点の個数」と「接線の本数」は同じですね!

厳密には一致しない場合があるけど・・・
まあそれは少し難しい話なので,ここではスルー!
少なくとも \(3\) 次関数を扱うときは必ず
「接点の個数」と「接線の本数」は一致するので,まとめると
「①の方程式の解の個数」と「接線の本数」が一致するということです。

つまり,\(a=-2p^3+3p^2+4\) ・・・①
の解の個数を考えればいいから,
両辺のグラフを考えて,交点の個数を確認すればいいですね!

\(\begin{cases}y=a\\y=-2p^3+3p^2+4\end{cases}\)
としてグラフをかいて交点の個数を確認しましょう!
このように,\(a=(p\) の式) の形にしてから考える方法を「定数分離型」と言います!
(2)解答
(1)より \(y=(3p^2-6p)x-2p^3+3p^2+4\) が 点 \(A(0,a)\) を通るので,
\(a=-2p^3+3p^2+4\) ・・・①
\(y=f(x)\) は \(3\) 次関数であるから,
①の実数解の実数解は,接点の \(x\) 座標を表すので,
①の実数解の個数と,点 \(A(0,a)\) ( ただし,\(a\) は実数 ) を通る \(C\) の接線の本数は一致する.
よって,
\(\begin{cases}y=a\\y=-2p^3+3p^2+4\end{cases}\)
の \(2\) つのグラフの交点の個数を考えればよい.
\(g(p)=-2p^3+3p^2+4\) とおくと
\(g^{\prime}(p)=-6p^2+6p=-6p(p-1)\)
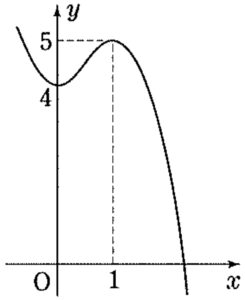 \(g(0)=4\) , \(g(1)=5\) より,\(y=g(p)\) のグラフは右図のようになるため,
\(g(0)=4\) , \(g(1)=5\) より,\(y=g(p)\) のグラフは右図のようになるため,
このグラフと \(y=a\) の共有点の個数に注目すると,
求める接線の本数は,
\(a<4\) または \(5<a\) のとき \(1\) 本
\(a=4\) , \(5\) のとき \(2\) 本
\(4<a<5\) のとき \(3\) 本








コメント