【問題】次の方程式の整数解をすべて求めよ.
(1) 2021 共通テスト
ああ① \(5x-3y=1\)
ああ② \(5x-3y=8\)
(2) 2019 センター試験
ああ\(49x-23y=1\)
考え方・解法手順
今回の(1)や(2)のような問題を「1次不定方程式」と言います.
解法手順が決まっていますので、しっかりと流れを身に付けましょう!
1次不定方程式以外の整数方程式については、【整数問題】整数方程式(積の形・範囲の絞り込み・解と係数の関係)にパターンものを全てまとめています!参考にしてください。
《Step1》解を1組みつける
例: \(( x , y )=( 2 , 3 )\) や \(( x , y )=( -1 , 2 )\) など、\(5x-3y=1\) に代入すると成立する.
何でも良いので、このような解を1組見つけることから始めましょう!
※このような解を「特殊解」という.
特殊解の見つけ方
① 頑張って探す
② ユークリッドの互除法の利用
③ 合同式の利用
最初は、「①頑張って探す」ことをお勧めします。見つかれば終わりです!いくつか値を代入し、実験して見つけましょう!
どうしても見つからなかった場合、「②ユークリッドの互除法の利用」または「③合同式の利用」を考えます。
「②ユークリッドの互除法を利用する」については後程解説.
※ ユークリッドの互除法はどうしても解答作成に時間がかかります。共通テストなど時間が少ない試験のことを考えると、時間短縮できる「③合同式の利用」が使えるようになることをオススメ!!
③合同式を利用した特殊解の見つけ方については⏬

《Step2》《Step1》で見つけた解を与式に代入し、差をとる
具体的にやっていきましょう!
【解答(1)①】
\(5x-3y=1\) ・・・(ア)
\(( x , y )=( 2 , 3 )\) は(ア)の解の1組より、
\(5\times2-3\times3=1\) ・・・(イ)
(ア)-(イ)より
\(5(x-2)-3(y-3)=0\)
\(5(x-2)=3(y-3)\) ・・・ (ウ)

右辺は3の倍数だから、左辺も3の倍数でなければダメ!
つまり、\(x-2\) が3の倍数になるね!
※3と5は互いに素であるから
整数 \(k\) を用いて、
\(x-2=3k\)
つまり \(x=3k+2\)
(ウ)に代入して、\(y=5k+3\)
※「3と5は互いに素であるから」について
3と5がお互いの倍数に影響しないからこそ、\(x-2\) が3の倍数であると言える.
ダメな例:\(6(x-2)=3(y-3)\) だった場合
右辺は3の倍数であるからと言って、\(x-2\) が3の倍数かどうかは分からない.
この場合は「6と3が互いに素でない」から
この1行は絶対に記述するように!
※記述がない場合、減点の可能性大!
【(1)の②について】
\(5x-3y=8\) に関しても、基本的には①と同様に
特殊解を、\(( x , y )=( 1 , -1 )\) として考えればよい.
ここでは、他の特殊解の見つけ方について紹介
\(ax+by≠1\) の特殊解の見つけ方について
まず、\(5x-3y=1\) の特殊解を探す.
→ \(( x , y )=( 2 , 3 )\)
\(5\times2-3\times3=1\) より、
両辺を8倍して
\(5\times16-3\times24=8\) となるため、
\(( x , y )=( 16 , 24 )\) は\(5x-3y=8\) の特殊解の1組となる.
※数字が大きくなった時、なかなか見つからないときに有効な手段
【解答(1)②】
\(5x-3y=8\) ・・・(ア)
\(5\times16-3\times24=8\) ・・・(イ)
(ア)-(イ)より
\(5(x-16)-3(y-24)=0\)
\(5(x-16)=3(y-24)\) ・・・ (ウ)
3と5は互いに素であるから
整数 \(k\) を用いて、
\(x-16=3k\)
つまり \(x=3k+16\)
(ウ)に代入して、\(y=5k+24\)
(2) 2019センター試験 \(49x-23y=1\) の整数解
【考え方】と【解答】

特殊解が見つからないよ・・・

そのようなときは、ユークリッド互除法を利用しましょう!
ユークリッド互除法
ユークリッドの互除法
2つの自然数 \(a , b\) について、\(a\) を \(b\) で割ったときの商を \(q\) 、余りを \(r\) とすると
「\(a\) と \(b\) の最大公約数」=「\(b\) と \(q\) の最大公約数」
\(49x-23y=1\) の係数の「49」と「23」に注目し
\(49 = 23\times2+3\) ・・・①
\(23 = 3\times7+2\) ・・・②
\(3 = 2\times1+1\) ・・・③
\(a=49 , b=23\) として①~③をそれぞれ「(余り)=~」の形に式変形すると、
①より \(3 = a-2b\) ・・・①´
②より \(2 = b-3\times7\) ・・・②´
③より \(1 = 3-2\times1\) ・・・③´
②´を③´に代入して
\(1 = 3-(b-3\times7)\times1\)
よって
\(1 = 3\times8-b\) に①´を代入すると
\(1 = (a-2b)\times8-b\)
したがって、
\(1 = 8a-17b\)
つまり、\(1 = 49\times8-23\times17\) ・・・④
(特殊解として、\(( x , y )=( 8 , 17 )\) であることが分かった.)
与式と④の差をとると、
\(49(x-8)-23(y-17)=0\)
\(49(x-8)=23(y-17) \)
49と23は互いに素であるから
整数 \(k\) を用いて、
\(x-8=23k\)
よって
\(x=23k+8\)
\(y=49k+17\)
(2)別解(格子点の利用)時短裏技
\(5x-3y=1\) の整数解とは、
\(y=\displaystyle\frac{5}{3}x-\displaystyle\frac{1}{3}\) という直線上の格子点を表す.
(※格子点・・・\(x\) 座標、\(y\) 座標ともに整数である平面上の点)
\(5x-3y=1\) は点 \(( 2 , 3 )\) を通り、傾き:\(\displaystyle\frac{5}{3}\) の直線を表す.
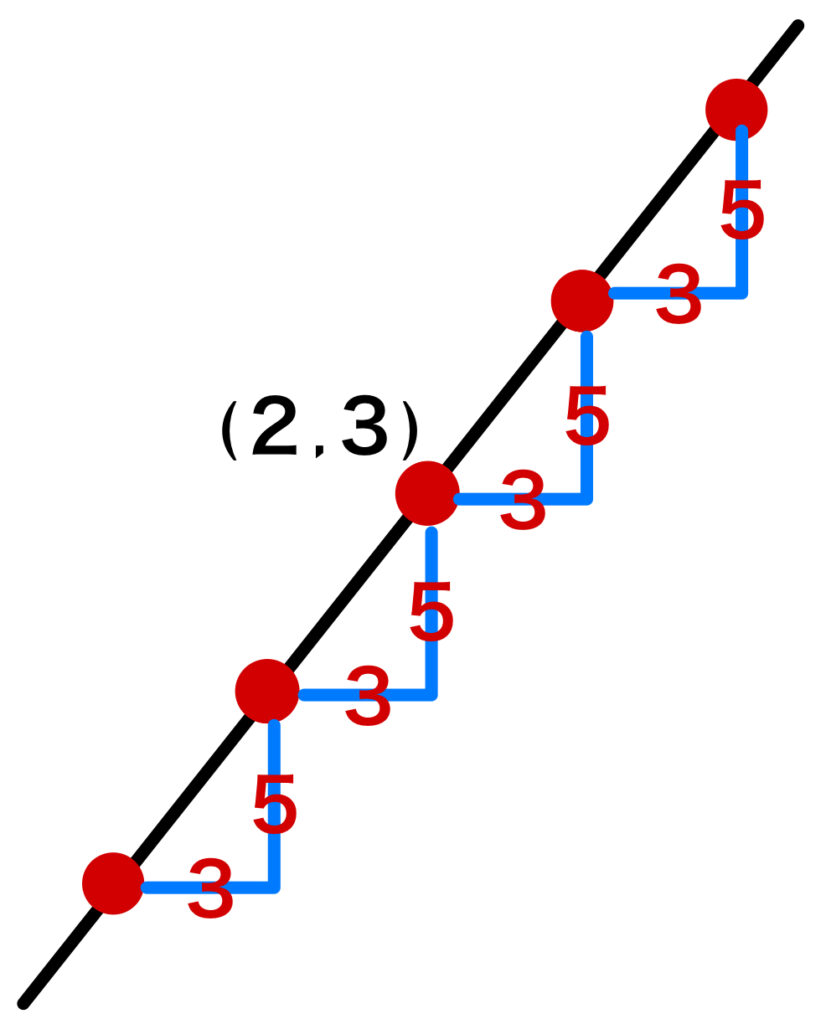
図より、
傾きに注目すると、
\(x\) 軸方向に3、\(y\) 軸方向に5だけ移動した点も格子点
(つまり整数解となる)ので、すべての格子点(整数解)は、点 \(( 2 , 3 )\) を基準として、\(x\) 軸方向に3の倍数、\(y\) 軸方向に5の倍数だけ移動した点となる.
よって整数 \(k\) を用いて、
\(x=3k+2\) , \(y=5k+3\) と分かる.
最後に(1次不定方程式以外の整数方程式について)
いかがだったでしょうか?
別解の格子点を利用した解法は学校の授業ではあまり学習しないかもしれません。しかし慣れると非常に早い解法になります。時短テクニックとして知っておきましょう!
1次不定方程式は、定期考査・共通テストなど頻出テーマ。それぞれの解法を理解し、手順を覚え、しっかりと処理できるように演習をしておきましょう!
また、1次方程式以外の整数方程式については、【整数問題】整数方程式(積の形・範囲の絞り込み・解と係数の関係)で確認しましょう!







コメント