例題
柿、リンゴ、ミカンの \(3\) 種類の果物の中から \(5\) 個の果物を買う.
次のような買い方は何通りあるか.
(1) 買わない果物があっても良い場合
(2) どの果物も少なくとも \(1\) 個は買う場合
重複組合せとは
重複(じゅうふく・ちょうふく)とは、同じものを何度も選んで良いということ。
つまり、重複組合せは「重複を許して」選ぶ組合せが何通りあるかを考えることです。
※数学では「じゅうふく」ではなく「ちょうふく」と読みます。
重複組合せの公式
種類のものから重複を許して 個選ぶ場合の数は
\({}_n \mathrm {H}_r = \displaystyle\frac{(n+r-1)!}{r!(n-r)!}\)
と計算できるのですが、この公式を覚えることはお勧めはしません。
しっかりと考え方をマスターし、様々な問題に応用できるようにしましょう!
例題
柿、リンゴ、ミカンの \(3\) 種類の果物の中から \(5\) 個の果物を買う.
次のような買い方は何通りあるか.
(1) 買わない果物があっても良い場合
(2) どの果物も少なくとも \(1\) 個は買う場合
(1)考え方
柿、リンゴ、ミカンをそれぞれ \(x\)、\(y\)、\(z\) 個買うとすると
\(x+y+z=5\) かつ \(x≧0\)、\(y≧0\)、\(z≧0\) を満たす \(x\)、\(y\)、\(z\) の組数を求めれば良い.
ここで、○ を \(5\) 個、|(仕切り) を \(2\) 本並べる方法を考えてみる.
例えば、「○○|○○|○」という並びを考えるとき、
下図のように、
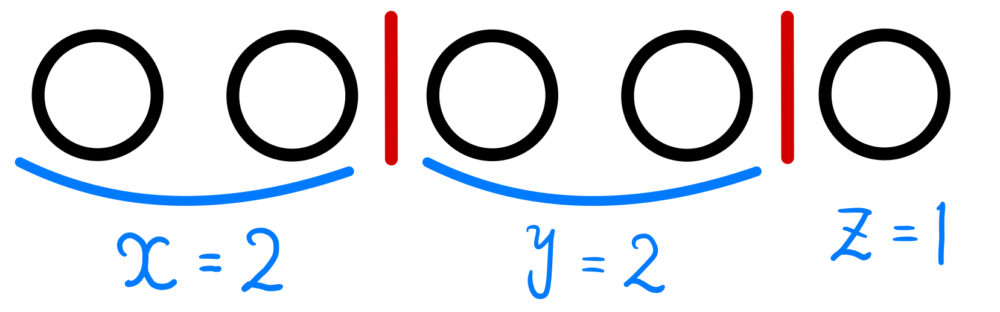
\(( x , y , z )=( 2 , 2 , 1 )\) と考えることができる.
他の例として
「○|○|○○○」→ \(( x , y , z )=( 1 , 1 , 3 )\)
「○○|○○○|」→ \(( x , y , z )=( 2 , 3 , 0 )\)
「○○||○○○」→ \(( x , y , z )=( 2 , 0 , 3 )\)
「○○○○○||」→ \(( x , y , z )=( 5 , 0 , 0 )\)
のようにカウントすることができる.
つまり、(1)の問題は、
○ を \(5\) 個、|(仕切り) を \(2\) 本並べる方法を考えればよい!
よって、\(\displaystyle\frac{7!}{5!2!}=21\) 通り
(2)考え方
柿、リンゴ、ミカンをそれぞれ \(x\)、\(y\)、\(z\) 個買うとすると
\(x+y+z=5\) かつ \(x≧1\)、\(y≧1\)、\(z≧1\) を満たす \(x\)、\(y\)、\(z\) の組数を求めれば良い.
(1)との違いは、\(0\) 個がダメ!ということ。
つまり、(1)の例で示したような、
「○○|○○○|」→ \(( x , y , z )=( 2 , 3 , 0 )\)
「○○||○○○」→ \(( x , y , z )=( 2 , 0 , 3 )\)
「○○○○○||」→ \(( x , y , z )=( 5 , 0 , 0 )\)
のような、|(仕切り)が両サイドにある場合や、連続して|(仕切り)が並ぶ場合がダメである.
よって、
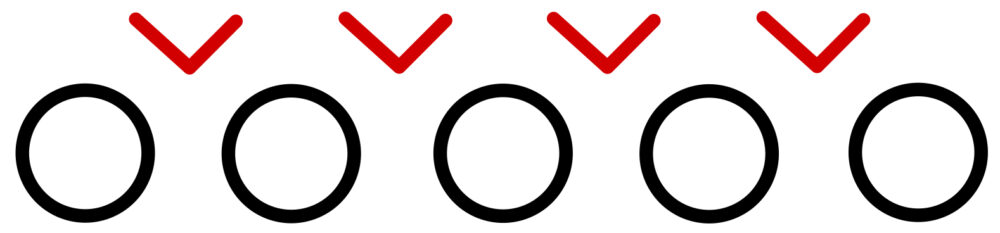
のように \(5\) 個の ○ の間の \(4\) カ所から \(2\) カ所選んで仕切りを入れれば良い.
したがって、\({}_4 C_2=6\) 通り
(2)別解
(2)は \(x+y+z=5\) かつ \(x≧1\)、\(y≧1\)、\(z≧1\) を満たす \(x\)、\(y\)、\(z\) の組数を求めれば良い.
ここで、\(x≧1\)、\(y≧1\)、\(z≧1\) より、
\(x-1≧0\)、\(y-1≧0\)、\(z-1≧0\) なので、
\(A=x-1\)、\(B=y-1\)、\(C=z-1\) とおくと、
\((A+1)+(B+1)+(C+1)=5\) かつ \(A≧0\)、\(B≧0\)、\(C≧0\) をみたす A、B、Cを考えればよい
したがって、(1)の考え方に帰着するので、
「 ○ を \(2\) 個、|(仕切り)を \(2\) 本並べる」ことを考えれば良い
よって、\(\displaystyle\frac{4!}{2!2!}=6\) 通り









コメント