【2022群馬大学・医学部】指数・対数関数の不等式と領域

解答・解説

\(\displaystyle\frac{2^{x+2}}{3^{y-2}}+\displaystyle\frac{3^y}{2^{x-1}}≦18\)

\(\iff\) \(\displaystyle\frac{2^2\cdot 2^{x}}{3^{-2}\cdot 3^{y}}+\displaystyle\frac{3^y}{2^{-1}\cdot 2^{x}}≦18\)

\(\iff\) \(36\cdot\displaystyle\frac{2^x}{3^y}+2\cdot\displaystyle\frac{3^y}{2^x}≦18\)

\(\iff\) \(18\cdot\displaystyle\frac{2^x}{3^y}+\displaystyle\frac{3^y}{2^x}≦9\)

\(t=\displaystyle\frac{2^x}{3^y}\) ( \(t>0\) ) とおくと

\(18t+\displaystyle\frac{1}{t}≦9\)

両辺を \(t\) ( \(>0\) ) 倍すると

\(18t^2-9t+1≦0\)

\((6t-1)(3t-1)≦0\)

\(\displaystyle\frac{1}{6}≦t≦\displaystyle\frac{1}{3}\)

\(\displaystyle\frac{1}{6}≦\displaystyle\frac{2^x}{3^y}≦\displaystyle\frac{1}{3}\)

\(\iff\) \(3\cdot 2^x ≦3^y≦6\cdot 2^x=3\cdot 2^{x+1}\)

底を \(3\) とする対数をとると

\((\log_{3}2)x+1≦y≦(\log_{3}2)x+\log_{3}2+1\)

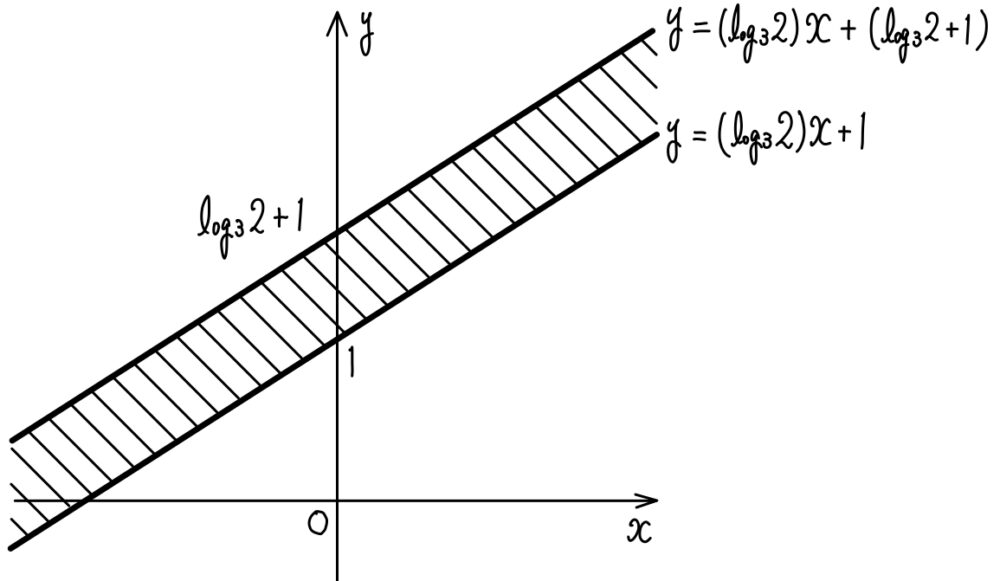
求める領域は上記の斜線部．ただし境界線を含む．