【2022京都大学・理・第2問】
箱の中に\(1\) から \(n\) までの番号がついた \(n\) 枚の札がある.ただし、\(n≧5\) とし、同じ番号の札はないとする.この箱から \(3\) 枚の札を同時に取り出し、札の番号を小さい順に \(X\)、\(Y\)、\(Z\) とする.このとき、\(Y-X≧2\) かつ \( Z-Y≧2\) となる確率を求めよ.
実験
条件を満たす場合の数を、\(a_{n}\) 通りと表す.
・\(n=5\) のとき

※上の表は、\(( X , Y , Z )=( 1 , 3 , 5 )\) を表すことにする.
よって、\(a_{5}=1\)
・\(n=6\) のとき
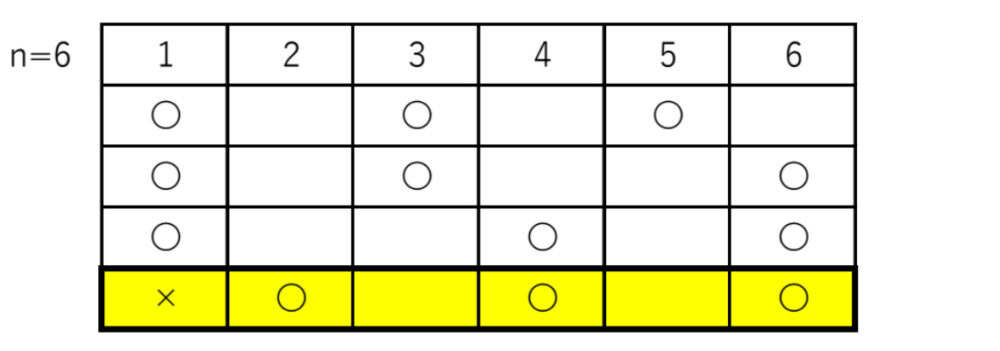
よって、\(a_{6}=4\)
・\(n=7\) のとき
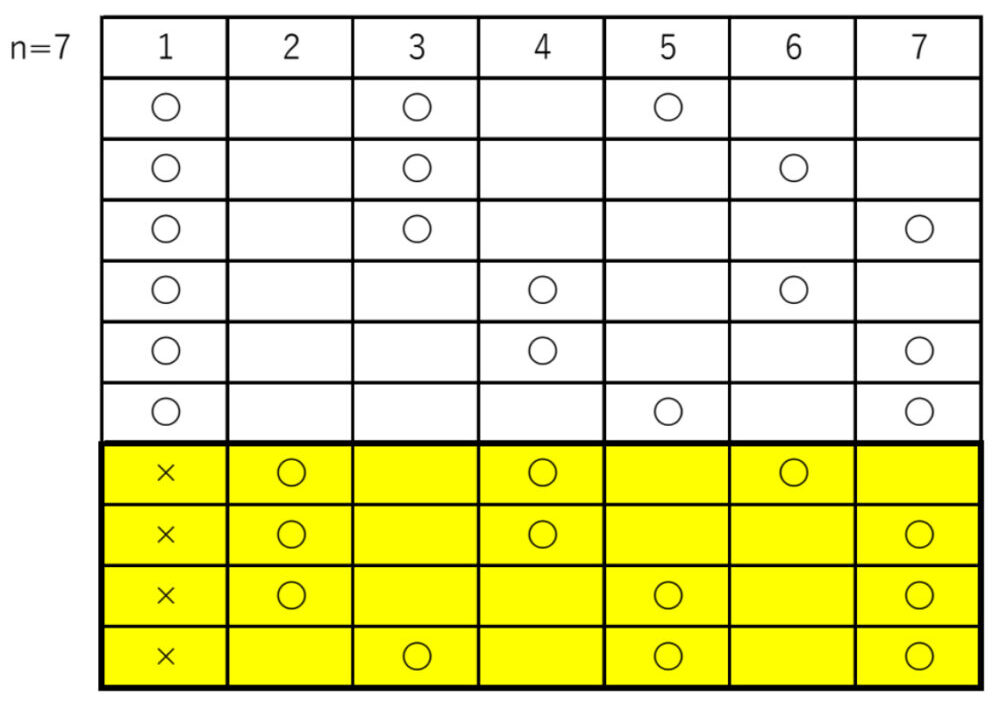
よって、\(a_{7}=10\)
\(n=7\) を考えた際、
\(X\not=1\) の場合(上の表の黄色の網掛け部分)は、\(a_{6}\) と同じ
つまり、\(a_{7}=a_{6}\)+( \(1~7\) の中で \(X=1\) のときの個数 ) となる.
つまり、
\(a_{n+1}=a_{n}\)+( \(1~(n+1)\) の中で \(X=1\) のときの個数 )
※ \(1~(n+1)\) の中で \(X=1\) のときの個数を考えればよい.
\(X=1\) のときを考える.
\(Y=3\) とすると、\(5≦Z≦n+1\) より、\((n+1)-5+1=n-3\) 個.
\(Y=4\) とすると、\(6≦Z≦n+1\) より、\((n+1)-6+1=n-4\) 個.
これを繰り返し、
\(Y=n-1\) とすると、\(Z=n+1\) より、\((n+1)-(n+1)+1=1\) 個.
よって、\((n-3)+(n-4)+\cdots+1\) を計算した個数が、\(X=1\) のときである.
( ☝ 初項が \(n-3\)、末項が \(1\)、項数 \(n-3\) の等差数列の和)
※上のように解答を作っても良いが、以下の解答では \(Y=k\) として、Σで計算して解答を作成しています.しっかりとイメージを持ったうえで解答を作りましょう!
解答
条件を満たす場合の数を、\(a_{n}\) 通りと表す.
\(1~(n+1)\) の中で \(X=1\) のとき
\(Y=k\) ( \(k= 3 , 4 , 5 , \cdots , n-1\) ) とおくと、
\(z≧k+2\) より、
\((n+1)-(k+2)+1=n-k\) 個
よって、
\(\displaystyle\sum_{k=3}^{n-1}{(n-k)}=\displaystyle\frac{1}{2}(n-3)(n-2)\) 個
したがって、
\(a_{n+1}=a_{n}+\displaystyle\frac{1}{2}(n-3)(n-2)\) ・・・① が成り立つ
\(a_{n}=a_{5}+\displaystyle\sum_{k=5}^{n-1}{\displaystyle\frac{1}{2}(k-3)(k-2) }\)
これを計算(※計算については下記に参考として紹介)すると
\(a_{n}=\displaystyle\frac{1}{6}(n-4)(n-3)(n-2)\)
以上より求める確率は、
\(\displaystyle\frac{a_{n}}{_{n}C_{3}}=\displaystyle\frac{(n-4)(n-3)}{n(n-1)}\)
※参考(Σの計算について)
連続する整数の積の和について
覚えておくと便利な公式
\(\displaystyle\sum_{k=1}^{n}{k(k+1)}= \displaystyle\frac{1}{3}n(n+1)(n+2)\)
※連続 \(2\) 整数の積の和⇒ \(3\) 分の \(1\) で、連続する \(3\) 整数の積
\(\displaystyle\sum_{k=1}^{n}{k(k+1)(k+2)}= \displaystyle\frac{1}{4}n(n+1)(n+2)(n+3)\)
※連続 \(3\) 整数の積の和⇒ \(4\) 分の \(1\) で、連続する \(4\) 整数の積
一般に、
『連続 \(n\) 整数の積の和⇒ \((n+1)\) 分の \(1\) で、連続する \((n+1)\) 整数の積』
の形になる.
(証明)※この計算過程も大切!
\(\displaystyle\sum_{k=1}^{n}{k(k+1)}= \displaystyle\frac{1}{3}n(n+1)(n+2)\) について
\(\displaystyle\sum_{k=1}^{n}{k(k+1)}\)
\(=\displaystyle\sum_{k=1}^{n}{k(k+1)\left\{(k+2)-(k-1)\right\}\times \displaystyle\frac{1}{3}}\)
\(=\displaystyle\frac{1}{3}\sum_{k=1}^{n}{\left\{k(k+1)(k+2)-(k-1)k(k+1)\right\}}\)
ここで、\(f(n)=(n-1)n(n+1)\) とおくと、
\(\displaystyle\sum_{k=1}^{n}{\left\{f(n+1)-f(n)\right\}}\)
\(=\left\{f(2)-f(1)\right\}+ \left\{f(3)-f(2)\right\}+ \left\{f(4)-f(3)\right\}+\cdots+\left\{f(n+1)-f(n)\right\}\)
\(=f(n+1)-f(1)\)
\(=n(n+1)(n+2)\) であるから、
したがって、
\(\displaystyle\sum_{k=1}^{n}{k(k+1)}= \displaystyle\frac{1}{3}n(n+1)(n+2)\)
これを利用すると、本問の
\(a_{n}=a_{5}+\displaystyle\sum_{k=5}^{n-1}{\displaystyle\frac{1}{2}(k-3)(k-2)}\) の計算については、
\(\displaystyle\sum_{k=5}^{n-1}{\displaystyle\frac{1}{2}(k-3)(k-2)}\)
\(=\displaystyle\frac{1}{6}\displaystyle\sum_{k=5}^{n-1}{\left\{(k-3)(k-2)(k-1)-(k-4)(k-3)(k-2)\right\}}\)
\(=\displaystyle\frac{1}{6}\left\{(n-4)(n-3)(n-2)-1\times2\times3\right\}\)
\(=\displaystyle\frac{1}{6}(n-4)(n-3)(n-2)-1\) となるため、
\(a_{n}=a_{5}+\displaystyle\sum_{k=5}^{n-1}{\displaystyle\frac{1}{2}(k-3)(k-2)}\) は、
\(=1+\displaystyle\frac{1}{6}(n-4)(n-3)(n-2)-1\)
\(=\displaystyle\frac{1}{6}(n-4)(n-3)(n-2)\)
と計算できる.
部分分数分解と同じ要領で計算することで、煩雑なΣ計算をしなくて済む.







コメント