【2022お茶の水女子大学・理・第1問】
\(a\) を実数として,曲線 \(y=\sin x\) の接線で点 \((2,a)\) を通るものを考える.以下の問いに答えよ.
(1) 点 \((2,a)\) を通る接線について,接点の \(x\) 座標を \(t\) とするとき,\(a\) を \(t\) を用いて表せ.
(2) (1)で求めた式を \(a=f(t)\) とおくとき,\(0≦t≦\displaystyle\frac{5\pi}{2}\) における \(f(t)\) の最大値と最小値を求めよ.
(3) 点 \((2,a)\) を通り,\(0≦t≦\displaystyle\frac{5\pi}{2}\) の範囲に接点の \(x\) 座標がある接線の本数が \(3\) 本となる \(a\) の範囲を求めよ.
考え方
接線の方程式
曲線 \(y=f(x)\) 上の点 \(A(a,f(a))\) における曲線の接線の方程式は
\(y-f(a)=f^{\prime}(a)(x-a)\)
接線何本引けるか問題

数学Ⅱ,Ⅲともに,外部の点から接線が何本ひけるかという問題は,毎年どこかの大学で出題される頻出・有名問題です!
解法の考え方・流れについては「【頻出・微分(数Ⅱ)】定数分離型・外部の点から3次関数のグラフに接線が何本引けるか?」を参考にしてください!
解答・解説
(1)
\(y^{\prime}=\cos x\) より,\((t,\sin t)\) における接線の方程式は
\(y-\sin t=\cos t(x-t)\)
よって,\(y=(\cos t)x-t\cos t+\sin t\) ・・・①
①が \((2,a)\) を通るので
\(a=(2-t)\cos t+\sin t\)
(2)
\(f(t)=(2-t)\cos t+\sin t\) より
\(f^{\prime}(t)=-\cos t+(2-t)(-\sin t)+\cos t=(t-2)\sin t\)
| \(t\) | \(0\) | \(2\) | \(\pi\) | \(2\pi\) | \(\displaystyle\frac{5\pi}{2}\) | ||||
| \(f^{\prime}(t)\) | \(0\) | ー | \(0\) | + | \(0\) | ー | \(0\) | + | |
| \(f(t)\) | \(2\) | ↘️ | \(\sin 2\) | ↗️ | \(\pi-2\) | ↘️ | \(2-2\pi\) | ↗️ | \(1\) |
したがって,
\(x=0\) で最大値 \(2\) ,\(x=2\pi\) で最大値 \(2-2\pi\)
(3)
(2)の増減表から,\(y=f(t)\) のグラフは下図のようになる
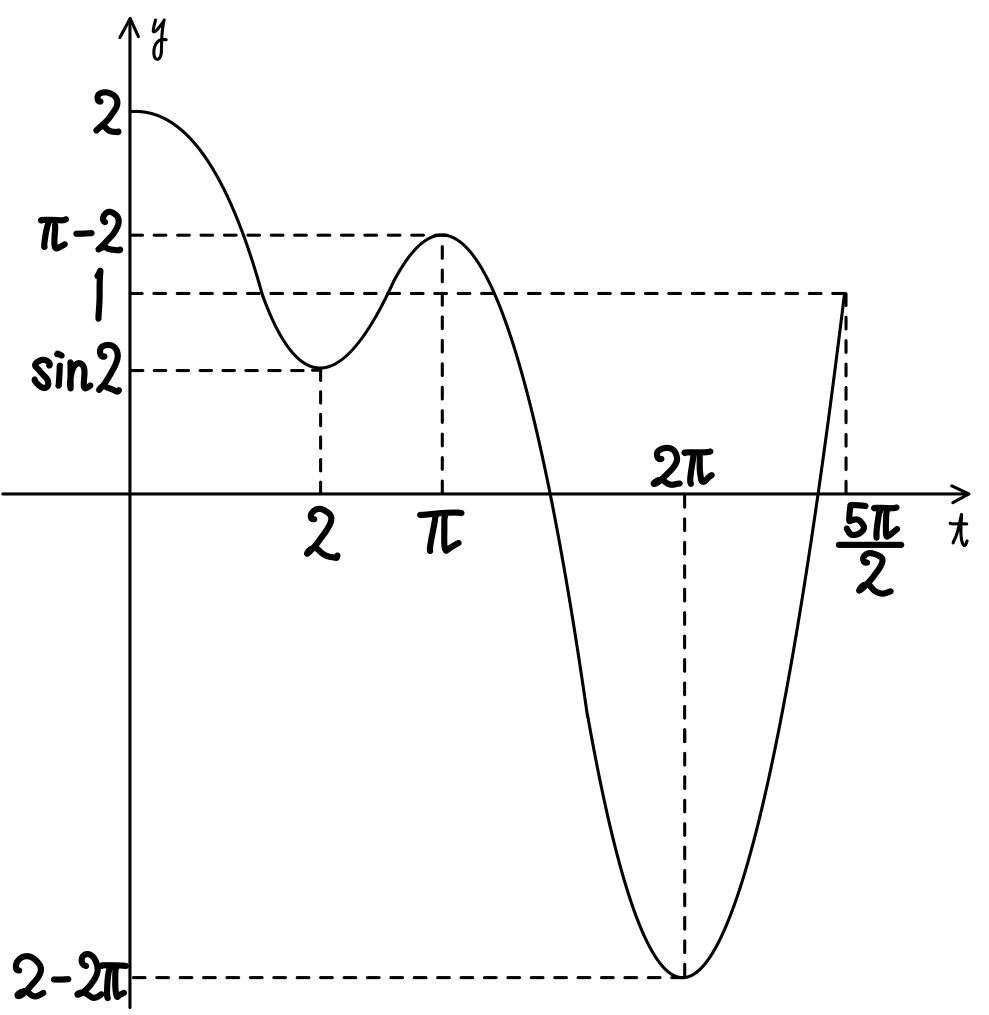
ここで対応関係に注意すると
\(t=\displaystyle\frac{\pi}{2},\displaystyle\frac{5\pi}{2}\) のときは接線が \(y=1\) となり一致.
それ以外のときは,\(t\) の値と接線の本数が \(1\) 対 \(1\) に対応する.
したがって,\(a=f(t)\) をみたす \(t\) が \(0≦t≦\displaystyle\frac{5\pi}{2}\) の範囲に \(3\) つ存在するときであるから
\(a=\sin 2\),\(1≦a<\pi-2\)







コメント