2022立命館大学・全学統一方式[文系2/2実施]

2月2日に実施された、立命館大学・全学統一方式(文系)の入試問題【整数問題】です。
文系で数学が苦手な人からすると、パッと見た感じたくさん記号が登場し、難しく見えるかもしれませんが、しっかりと「具体化」や整数問題の極意である「実験」を行うことで、簡単に処理することが出来る問題です。
これからまだ私立受験、国公立2次試験を控える受験生や、数学Aの整数の分野を学習済みの高校1、2年にとってもよい演習問題となります。
このような基本問題をしっかりと勉強し、実力アップをしていきましょう!
考え方・方針の立て方
(a) について
ただただ \(50\) 以下の素数を書き並べることで答えが求まります。
(b) について
下記でも行いますが、具体的に実験を行いましょう!
(c) について
合同式が利用できると、解答がスッキリ&早く処理できます。
新しい記号などに抵抗がある人が多いですが、様々な計算をしなくて済む、便利な道具です。特に整数問題においては必須アイテム!
合同式に不安がある人は、
を確認してみてください。
集合の記号についての確認
集合の表し方について
集合の表し方は2つあります。
① 要素を{ }の中に書き並べる方法
② { }の中に | (縦線)を書き、縦線よりも右側に \(x\) のみたす条件を書く方法
例:\(1\) 桁の偶数の集合 \(A\) は
①の場合は、\(A=\left\{ 2 , 4 , 6 , 8 \right\}\)
②の場合は、\(A=\left\{ 2x | 1≦x≦4 , x は整数 \right\}\)
ちなみにこのとき、集合 \(A\) は \(4\) 個の要素を持つので、\(n(A)=4\) と表せる.
かつ、または、包含関係などの記号
2つの集合 \(A\)、\(B\) に対して、
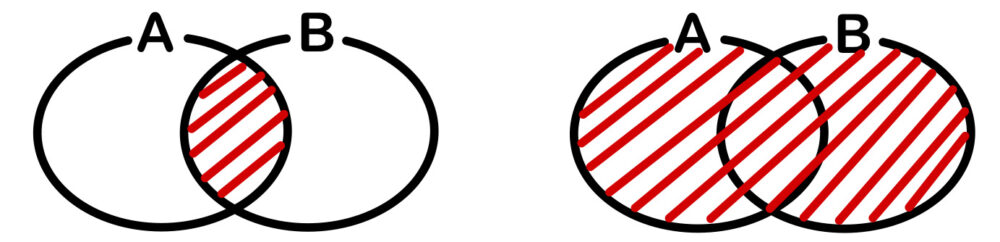
・上左図の赤の斜線部分を、\(A\cap B\) で表し、共通部分という.
・上右図の赤の斜線部分を、\(A\cup B\) で表し、和集合という.
※\(n(A\cup B)=n(A)+n(B)-n(A\cap B)\) の関係が成り立つ.
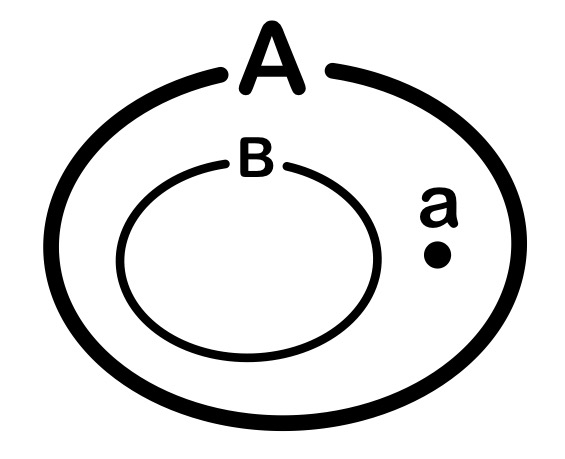
右図のような2つの集合 \(A\)、\(B\) に対して、
集合 \(A\) に集合 \(B\) が含まれるとき、
\(A\supset B\) と表す.
また、要素 \(a\) が集合 \(A\) に属し、集合 \(B\) に属さないとき、
\(a\in A\)、\(a\notin B\) と表す.
![]()
整数問題の極意は実験!
この問題を見て、特に何も迷うことなく問題が解ける人はスルーしてください。
方針が今一見えない方は、しっかりと実験(具体的な値で考える)をしましょう!
整数問題の多くは、実験をすることで規則や法則、方針や答えが見えてきます。
実験
(b) について
それでは具体的な値で実験をしていきましょう!
例えば、\(k=0\) とすると
\(B_{0}=\left\{q | q=7m , m は整数 \right\}\)
つまり、\(50\) 以下の自然数が全体集合であることに注意すれば、
\(B_{0}=\left\{ 7 , 14 , 21 , 28 , 35 , 42 , 49 \right\}\) となるので、
\(n\left(B_{0}\right)=7\) ( \(7\) 個の要素 ) となる.
このように \(k = 1 , 2 , \cdots\) と調べた上で、最も要素の個数が多いものを求めなさいと言う問題です。
解答
(a)~(c) の解答
まず初めに、自然数 \(1\) ~ \(50\) を下の表のようにまとめる.
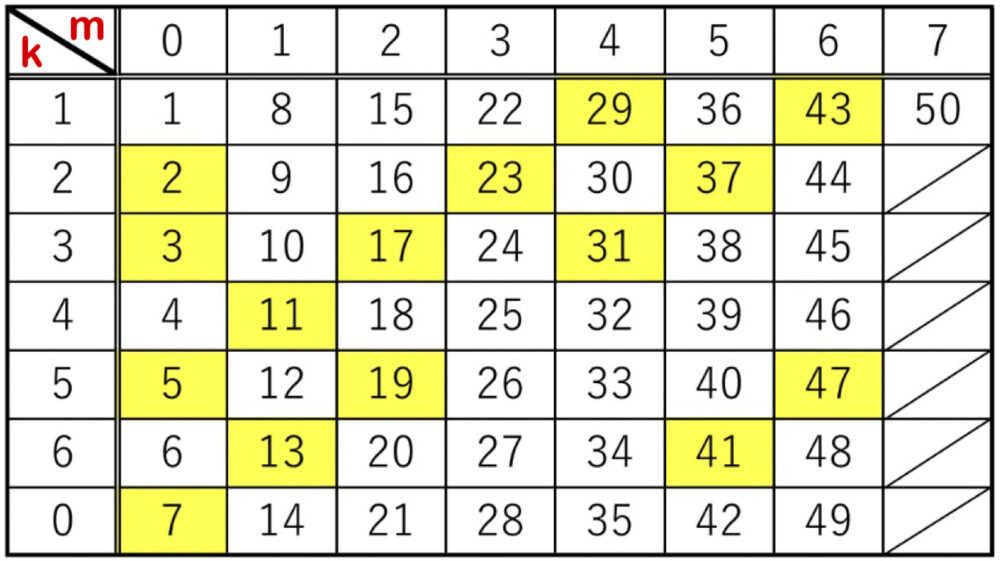
(a) 自然数 \(1\) ~ \(50\) の中で素数である数は、上の表の背景を黄色で表した数字であるから、
\(n(A)=15\)
(b) 上の表より、\(1\) 段目 ( \(k=1\) ) のとき、最も要素の個数が多くなる.
したがって、\(n(B_{k})\) が最大となる \(k=1\)
\(k=1\) のとき
\(n(B_{1})=8\)、\(n(A\cap B_{1})=2\)、また (a) の結果と
\(n(A\cup B_{1})=n(A)+n(B_{1})-n(A\cap B_{1})\) より
\(n(A\cup B_{1})=15+8-2=21\)
(c) \(x\in B_{3}\)、\(y\in B_{5}\) より、整数 \(s , t\) を用いて、
\(x=7s+3\)、\(y=7t+5\) とおくことができる.
\(x\times y=(7s+3)(7t+5)=7(7st+5s+3t+2)+1\) であるから、
\(x\times y\) を \(7\) で割った余りは \(1\)
上と同じように、
\(x\in B_{3}\) より \(x=7s+3\) とおき、
\(a\) が \(B_{1}\)、\(B_{2}\)、\(B_{3}\)、・・・と1つ1つ確認すれば答えは求まる.
しかしこれはなかなか大変であるので、ここで合同式を利用して解答を作成する.
(c) について:合同式を利用した解答
以下すべて、mod 7 として考える.
\(x\in B_{3}\)、\(y\in B_{5}\) より、
\(x≡3\)、\(y≡5\) であるから、
\(xy≡3\times 5=15≡1\)
したがって、\(x\times y\) を \(7\) で割った余りは \(1\)
\(x\in B_{3}\) より \(x≡3\)
・\(a≡1\) のとき \(ax≡3\) となり条件を満たす.
・\(a≡2\) のとき \(ax≡6\) となり条件を満たさない.
・\(a≡3\) のとき \(ax≡9≡2\) となり条件を満たさない.
・\(a≡4\) のとき \(ax≡12≡5\) となり条件を満たさない.
・\(a≡5\) のとき \(ax≡15≡1\) となり条件を満たさない.
・\(a≡6\) のとき \(ax≡18≡4\) となり条件を満たさない.
・\(a≡0\) のとき \(ax≡0\) となり条件を満たさない.
したがって、条件を満たすのは \(a≡1\) のとき
つまり、\(k=1\) を満たす中の素数を考えればよいので、
求める \(a\) の値は、\(a = 29 , 43\)
■□━━ 急げ、ドメインは早い者勝ち! ━━□■
■お名前.com ![]()







コメント