【2022東京医科歯科大学・医学部・第3問】
曲線 \(C\):\(y=f(x)\) ( \(0≦x<1\) ) が次の条件を満たすとする.
・\(f(0)=0\)
・\(0<x<1\) のとき \(f^{\prime}(x)>0\)
・\(0<a<1\) を満たすすべての実数 \(a\) について,曲線 \(C\) 上の点 \(P(a,f(a))\) における接線と直線 \(x=1\) との交点を \(Q\) とするとき,\(PQ=1\)
このとき以下の問いに答えよ.
(1) \(f^{\prime}(x)\) を求めよ.
(2) \(\displaystyle\int^{\frac{1}{2}}_{0}(1-x)f^{\prime}(x) dx\) の値を求めよ.
(3) 曲線 \(C\) と \(x\) 軸,直線 \(x=1\),直線 \(y=f\left(\displaystyle\frac{1}{2}\right)\) で囲まれた図形の面積を求めよ.
解答・解説
(1) \(f^{\prime}(x)\)
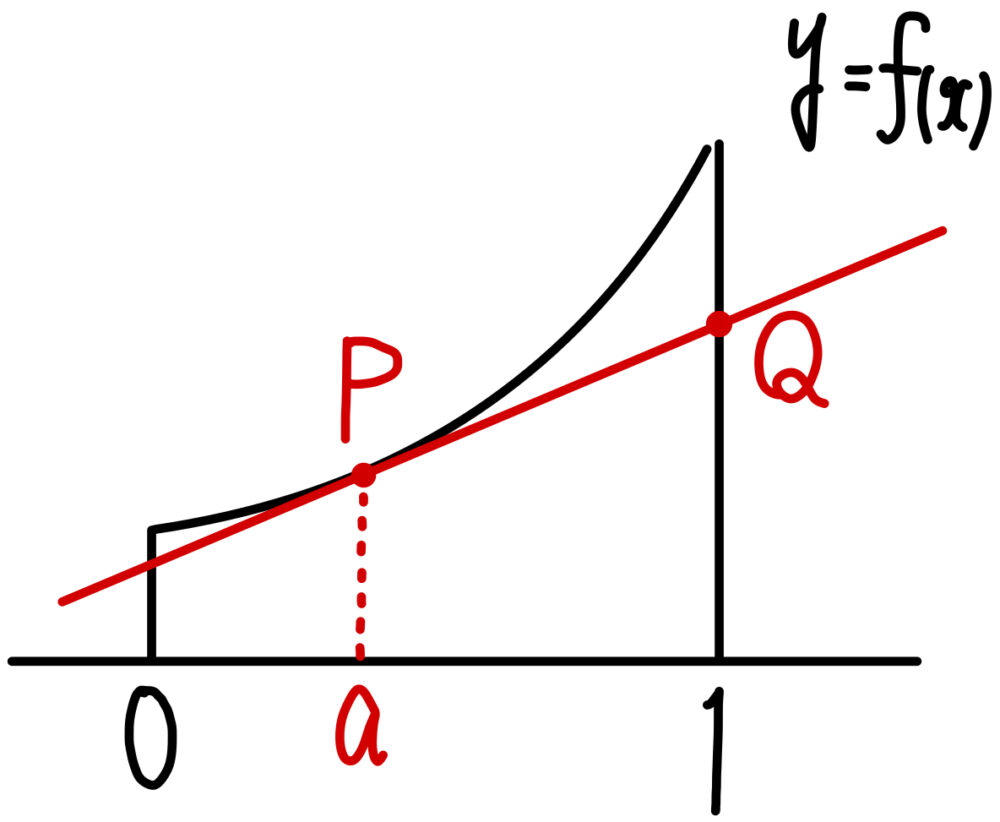

右図はあくまでもイメージ!
\(f^{\prime}(x)>0\) であるから,\(f(x)\) のグラフが単調増加であることはわかります!
点 \(P\) における接線の方程式は,
\(y-f(a)=f^{\prime}(a)(x-a)\)
よって,\(y=f^{\prime}(a)x-af^{\prime}(a)+f(a)\) ・・・①
①と \(x=1\) の交点が \(Q\) より
\(Q(1,f^{\prime}(a)-af^{\prime}(a)+f(a))\)
条件から \(PQ=1\) より \(PQ^2=1\)
\((1-a)^2+\left\{f^{\prime}(a)-af^{\prime}(a)\right\}^2=1\)
\((1-a)^2+(1-a)^2\left\{f^{\prime}(a)\right\}^2=1\)
\(\left\{f^{\prime}(a)\right\}^2=\displaystyle\frac{1}{(1-a)^2}-1\)
\(0<a<1\) のとき \(f^{\prime}(a)>0\) より
\(f^{\prime}(a)=\sqrt{\displaystyle\frac{1}{(1-a)^2}-1}\)
したがって,\(f^{\prime}(x)=\sqrt{\displaystyle\frac{1}{(1-x)^2}-1}\)
(2) \(\displaystyle\int^{\frac{1}{2}}_{0}(1-x)f^{\prime}(x) dx\)
(1)より
\(\displaystyle\int^{\frac{1}{2}}_{0}(1-x)f^{\prime}(x) dx\)
\(=\displaystyle\int^{\frac{1}{2}}_{0}(1-x)\sqrt{\displaystyle\frac{1}{(1-x)^2}-1}dx\)
\(=\displaystyle\int^{\frac{1}{2}}_{0}\sqrt{1-(1-x)^2}dx\)
\(=\displaystyle\int^{\frac{1}{2}}_{0}\sqrt{1-(x-1)^2}dx\)
 \(t=x-1\) とおくと与式は,
\(t=x-1\) とおくと与式は,
\(\displaystyle\int^{-\frac{1}{2}}_{-1}\sqrt{1-t^2} dt\)
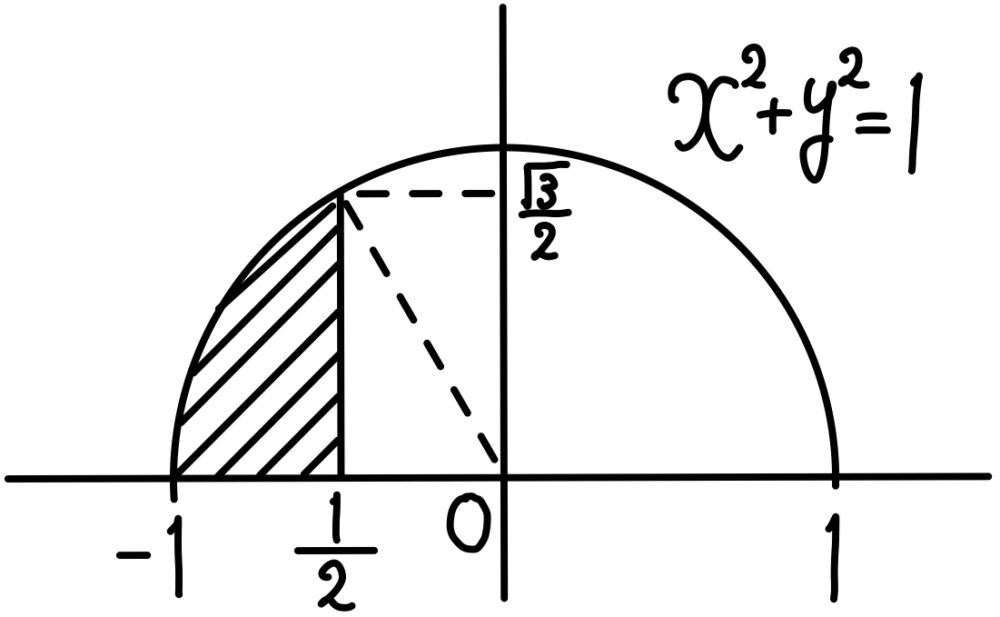
これは,中心原点,半径 \(1\) の円の右図の斜線部の面積を表すので,
\(\displaystyle\frac{1}{2}\cdot 1^2\cdot \displaystyle\frac{\pi}{3}-\displaystyle\frac{1}{2}\cdot\displaystyle\frac{1}{2}\cdot\displaystyle\frac{\sqrt{3}}{2}=\displaystyle\frac{\pi}{6}-\displaystyle\frac{\sqrt{3}}{8}\)
したがって,
\(\displaystyle\int^{\frac{1}{2}}_{0}(1-x)f^{\prime}(x) dx=\displaystyle\frac{\pi}{6}-\displaystyle\frac{\sqrt{3}}{8}\)
(3) 囲まれた図形の面積
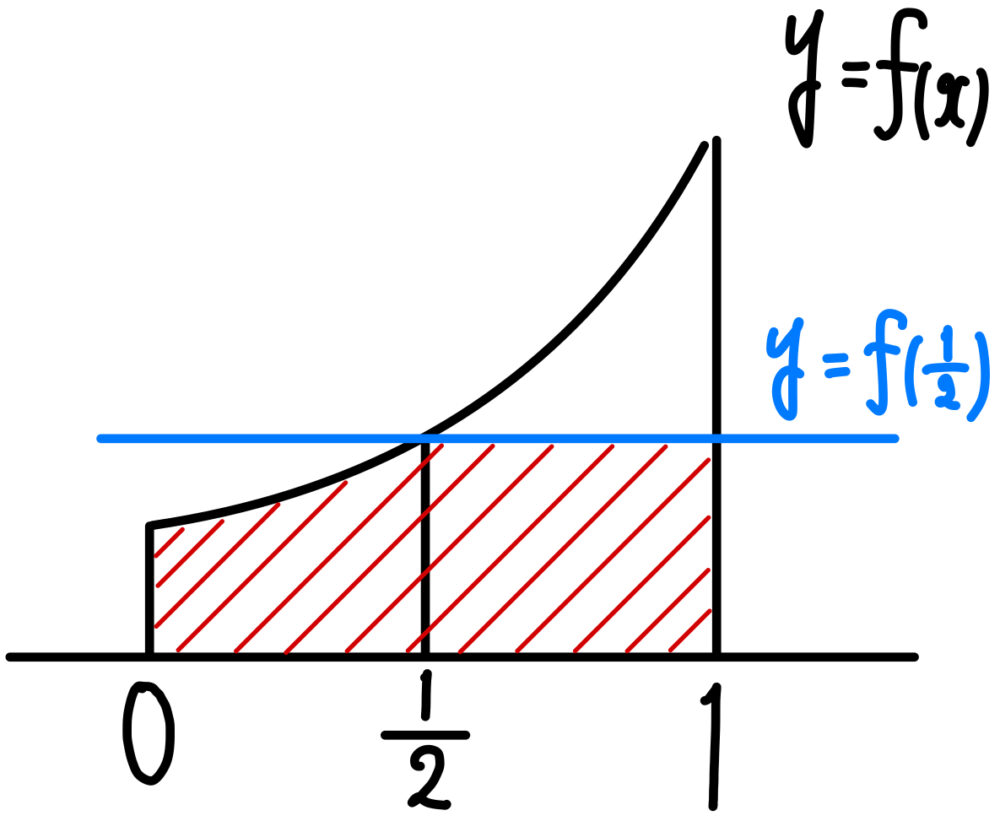
求める図形の面積を \(S\) とおくと
\(S=\displaystyle\int^{\frac{1}{2}}_{0} f(x)dx+\displaystyle\frac{1}{2}f\left(\displaystyle\frac{1}{2}\right)\)

(2)の結果を上手に利用したい!と思えるかどうかがPointです!部分積分を利用し,(2)の結果が利用できるように計算していきましょう!
\(S=\displaystyle\int^{\frac{1}{2}}_{0}(x-1)^{\prime} f(x)dx+\displaystyle\frac{1}{2}f\left(\displaystyle\frac{1}{2}\right)\)
\(=\Bigl[(x-1)f(x)\Bigr]^{\frac{1}{2}}_{0}-\displaystyle\int^{\frac{1}{2}}_{0}(x-1)f^{\prime}(x) dx+\displaystyle\frac{1}{2}f\left(\displaystyle\frac{1}{2}\right)\)
\(=-\displaystyle\frac{1}{2}f\left(\displaystyle\frac{1}{2}\right)+f(0)+\displaystyle\int^{\frac{1}{2}}_{0}(1-x)f^{\prime}(x) dx+\displaystyle\frac{1}{2}f\left(\displaystyle\frac{1}{2}\right)\)
\(f(0)=0\),(2)の結果より
\(S=\displaystyle\int^{\frac{1}{2}}_{0}(1-x)f^{\prime}(x) dx=\displaystyle\frac{\pi}{6}-\displaystyle\frac{\sqrt{3}}{8}\)







コメント