【2022山口大学】aのb乗=bのa乗(a^b=b^a)を満たす正の整数(a≠b)

【2013一橋大学・後期】eのπ乗とπのe乗の大小比較

e^πとπ^eの大小について、logx/xのグラフを利用することで考える。頻出・有名入試問題。差がつく良問ですので、流れを一度経験し、類題に対応できるように対策をしておきましょう！ 2013一橋大学・後期。２次試験過去問対策。数学Ⅲ：微分

mathmathmanabu.com

2022.10.03

解答・解説

(１) $x>0$ のとき，$f(x)=\displaystyle\frac{\log{x}}{x}$ の最大値

$f(x)=\displaystyle\frac{\log x}{x}$ ( $x>0$ )

$f^{\prime}(x)=\displaystyle\frac{1-\log x}{x^2}$ より

$f^{\prime}(x)=0$ とすると

$\log x=1$ $\iff$ $x=e$

よって，$y=f(x)$ は $x>0$ において

$x=e$ のとき，最大値 $\displaystyle\frac{1}{e}$

(２) $a^b=b^a$ かつ $a\not=b$ を満たす正の整数の組 $(a,b)$

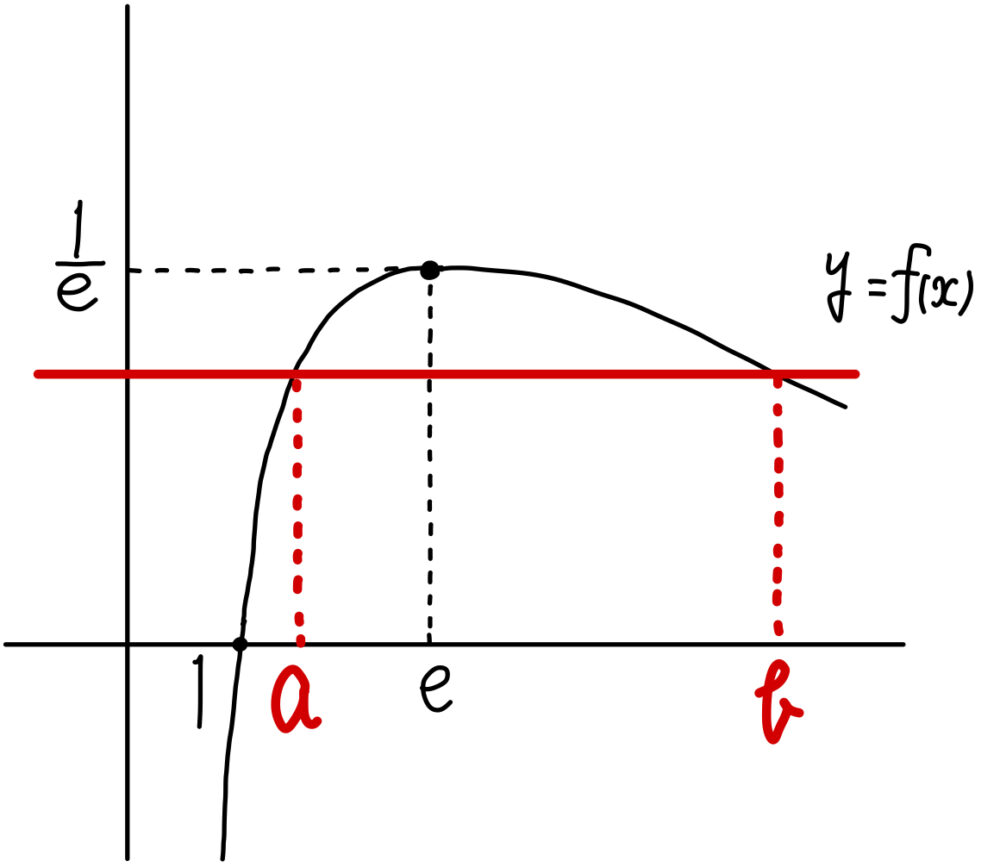$\displaystyle\lim_{x\rightarrow +0}f(x)=-\infty$ ，$\displaystyle\lim_{x\rightarrow\infty}f(x)=0$ より，関数 $y=f(x)$ のグラフの概形は右図(黒線部分)のようになる．

$\displaystyle\lim_{x\rightarrow\infty}f(x)=0$ については頻出の極限問題！証明とセットで覚えておきましょう！証明等については，⏬(下の記事)を参考に！

x→∞のときlogx/xの極限についての証明

x>1のとき0<logx<√xの不等式評価の証明と、頻出・重要問題のlogx/xの極限値について。グラフの図示や極限、不等式の証明など利用する場面は多々。数学Ⅲ：対数の極限

mathmathmanabu.com

2023.01.22

$a^b=b^a$ の両辺に自然対数をとると

$\log{a^b}=\log{a^b}$

$\iff$ $b\log{a}=a\log{b}$

$\iff$ $\displaystyle\frac{\log{a}}{a}=\displaystyle\frac{\log{b}}{b}$

よって $f(a)=f(b)$

$b>a>0$ とすると，右上図(赤線部分)に注目すると，

$1<a<e$ となり，これを満たす正の整数 $a=2$ のみ

このとき，

$f(2)=\displaystyle\frac{\log2}{2}=\displaystyle\frac{2\log2}{4}=\displaystyle\frac{\log4}{4}=f(4)$ であるから，

題意を満たす正の整数の組 $(a,b)=(2,4)$

$a>b>0$ のときも同様に考え，$(a,b)=(4,2)$

したがって，$(a,b)=(2,4),(4,2)$