【2023九州大学・理系・第1問】
以下の問いに答えよ.
(1) \(4\) 次方程式 \(x^4-2x^3+3x^2-2x+1=0\) を解け.
(2) 複素数平面上の \(\triangle ABC\) の頂点を表す複素数をそれぞれ \(\alpha\),\(\beta\),\(\gamma\) とする.
\((\alpha-\beta)^4+(\beta-\gamma)^4+(\gamma-\alpha)^4=0\)
が成り立つとき,\(\triangle ABC\) はどのような三角形になるか答えよ.
考え方・方針
相反方程式について

方程式の係数に注目してみましょう!
「\(1\) , \(-2\) , \(3\) , \(-2\) , \(1\)」と係数が左右対称になる方程式を相反方程式といいます。相反方程式は解法の手順が決まっていますので,しっかりとマスターしましょう!
相反方程式の解法手順
・最高次が偶数のとき \(x^{2n}+\cdots=0\)
👉 \(x^n\) で割って、\(t=x+\displaystyle\frac{1}{x}\) と置き換え
・最高次が奇数のとき \(x^{2n+1}+\cdots=0\)
👉 \(x+1\) を因数にもつ
つまり、\(x+1\) と 最高次が偶数の相反方程式に分解できる


一般の点を中心とする回転
点 \(\alpha\) を中心に、点 \(\beta\) を \(k\) 倍して、角 \(\theta\) だけ回転した点が \(\gamma\) のとき
\(\gamma-\alpha=k(\cos \theta+i \sin \theta) (\beta-\alpha)\)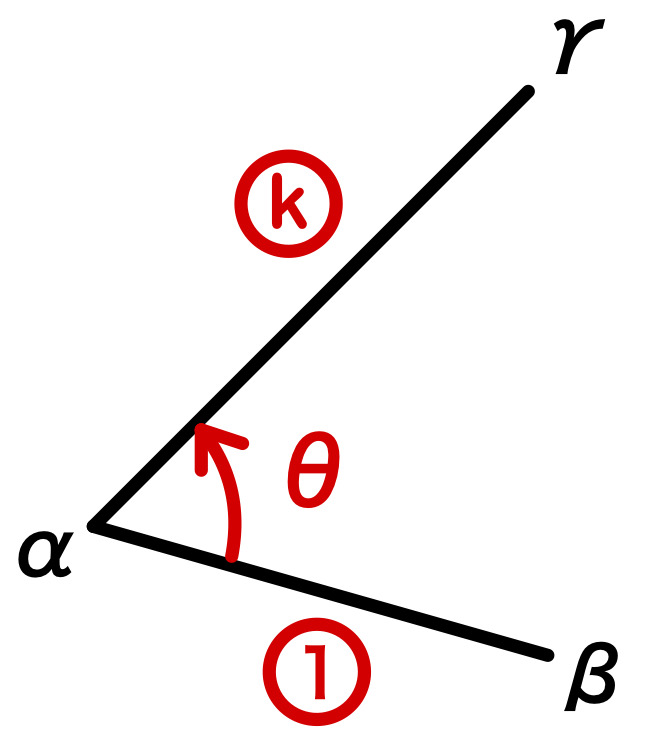
または
\(\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=k(\cos \theta+i \sin \theta)\)

\(\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=k(\cos \theta+i \sin \theta)\)
の形を作ることが出来れば,三角形の形状を掴むことができます!


解答・解説
(1) \(4\) 次方程式 \(x^4-2x^3+3x^2-2x+1=0\) を解け.
\(x^4-2x^3+3x^2-2x+1=0\) ・・・①
①は \(x=0\) を解に持たないので \(x^2\) で割ると
\(x^2-2x+3-\displaystyle\frac{2}{x}+\displaystyle\frac{1}{x^2}=0\)
\(\left(x^2+\displaystyle\frac{1}{x^2}\right)-2\left(x+\displaystyle\frac{1}{x}\right)+3=0\)
\(\left\{\left(x+\displaystyle\frac{1}{x}\right)^2-2\right\}-2\left(x+\displaystyle\frac{1}{x}\right)+3=0\)
\(\left(x+\displaystyle\frac{1}{x}\right)^2-2\left(x+\displaystyle\frac{1}{x}\right)+1=0\)
\(\left(x+\displaystyle\frac{1}{x}-1\right)^2=0\)
\(x+\displaystyle\frac{1}{x}-1=0\)
\(x^2-x+1=0\)
\(x=\displaystyle\frac{1\pm\sqrt{3}i}{2}\)
(2) \(\triangle ABC\) はどのような三角形になるか
\((\alpha-\beta)^4+(\beta-\gamma)^4+(\gamma-\alpha)^4=0\) より
\((\beta-\alpha)^4+\left\{(\beta-\alpha)-(\gamma-\alpha)\right\}^4+(\gamma-\alpha)^4=0\)
\(\alpha\not=\beta\) より \((\beta-\alpha)^4\) で割ると
\(1+\left(1-\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}\right)^4+\left(\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}\right)^4=0\)
ここで,\(z=\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}\) とおくと
\(1+(1-z)^4+z^4=0\)
\(z^4-2z^3+3z^2-2z+1=0\)
(1)の結果から
\(z=\displaystyle\frac{1\pm\sqrt{3}i}{2}\)
\(\displaystyle\frac{\gamma-\alpha}{\beta-\alpha}=\cos\left(\pm\displaystyle\frac{\pi}{3}\right)+i\sin\left(\pm\displaystyle\frac{\pi}{3}\right)\) (複号同順)
よって点 \(\gamma\) は \(\alpha\) を中心に \(\beta\) を \(\pm\displaystyle\frac{\pi}{3}\) 回転した点なので,
したがって \(\triangle ABC\) は正三角形となる.







コメント