
\(\cos 36\text{°}\) の値を求めよ.
【解法①】2倍角、3倍角の公式利用
\(\theta=36\text{°}\) とおく.
\(5\theta=180\text{°}\) より

次の式変形はぜひ覚えておこう!
\(3\theta=180\text{°}-2\theta\)
\(\cos 3\theta=\cos (180\text{°}-2\theta)=-\cos 2\theta\) ・・・①
2 倍角の公式 \(\cos 2\theta=2\cos^2\theta-1\)
3 倍角の公式 \(\cos 3\theta=4\cos^3\theta-3\cos \theta\)
を①に代入して、
\(4\cos^3\theta-3cos \theta=-(2\cos^2\theta-1)\)
\(4\cos^3\theta+2\cos^2\theta-3cos \theta-1=0\)
\(x=\cos \theta\) とおくと、\(\theta=36\text{°}\) より \(0<x<1\)
\(4x^3+2x^2-3x-1=0\)
左辺を \(f(x)\) とおくと
\(f(-1)=0\) なので
\((x+1)(4x^2-2x-1)=0\)
\(x=-1\)、\(\displaystyle\frac{1\pm\sqrt{5}}{4}\)
\(0<x<1\) より
\(x=\displaystyle\frac{1+\sqrt{5}}{4}\)
したがって、\(\cos 36\text{°}=\displaystyle\frac{1+\sqrt{5}}{4}\)
【解法②】二等辺三角形で余弦定理
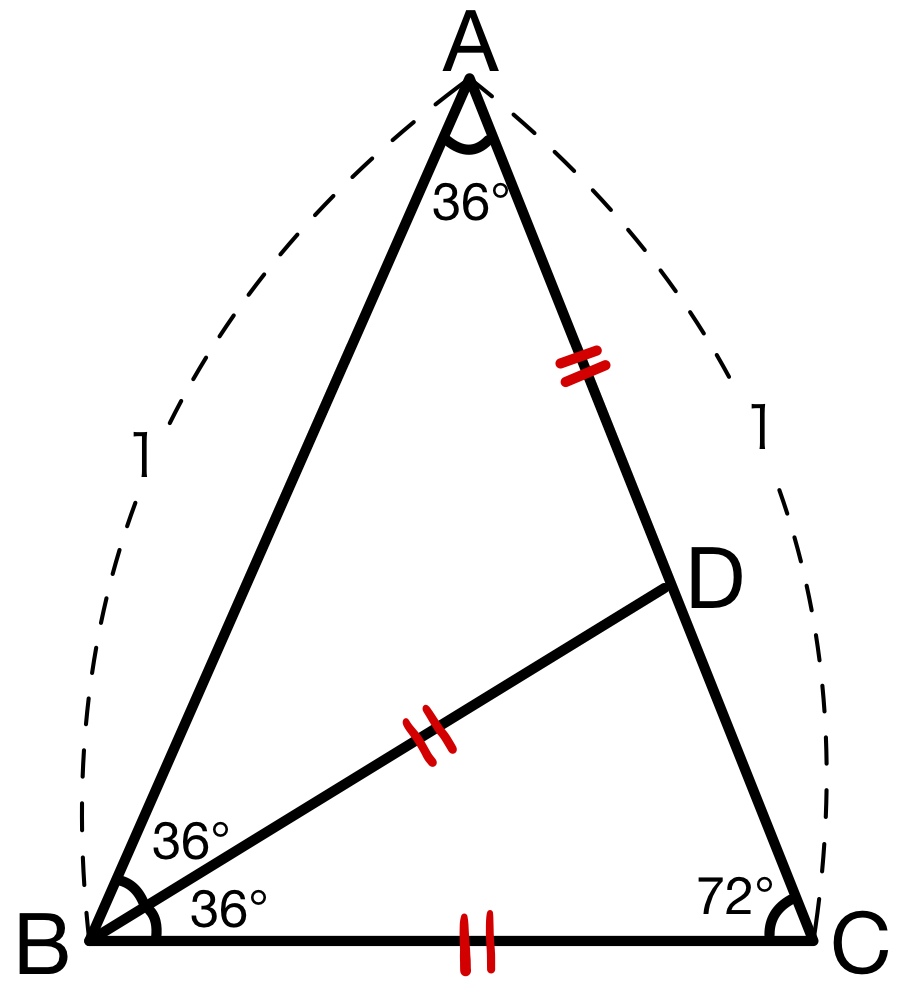
上図のような二等辺三角形を考え、線分 \(BD\) は、\(\angle B\) の二等分線とする。
\(BC=x\) とおくと
\(\triangle BCD\) は 二等辺三角形より、\(BC=BD=x\)
また、
\(\triangle ABD\) は二等辺三角形より、 \(AD=BD\)
よって、\(AD=x\) より、\(CD=1-x\)
\(\triangle ABC\sim\triangle BCD\) より
\(AB:BC=BC:CD\)
\(1:x=x:1-x\)
\(x^2+x-1=0\) ・・・②
\(x=\displaystyle\frac{-1\pm\sqrt{5}}{2}\)
\(x>0\) より、\(x=\displaystyle\frac{-1+\sqrt{5}}{2}\) ・・・③
次に、\(\triangle ABC\) で余弦定理から、
\(\cos 36\text{°}=\displaystyle\frac{1^2+1^2-x^2}{2\cdot 1\cdot 1}=\displaystyle\frac{2-x^2}{2}\)
②より、\(x^2=1-x\) なので
\(\cos 36\text{°}=\displaystyle\frac{x+1}{2}\)
③を代入すると、
\(\cos 36\text{°}=\displaystyle\frac{1+\sqrt{5}}{4}\)
まとめ
\(\cos 36\text{°}\) を求める作業は、様々な問題で活用できます。
例えば、
【解法①】の
\(5\theta=180\text{°}\) より
\(3\theta=180\text{°}-2\theta\)
のように、何倍かすることで有名角に持ち込み、\(\theta\) の一部を移行して処理をしていく流れや、
【解法②】については、正五角形の図形の一部として、図形の問題は当然、ベクトル分野など、様々なジャンルで出題されます。
とても有名な解法2つになりますので、しっかりと流れを理解し、他の問題にも応用できるように、自分のものにしてください!







コメント