【2021 近畿大学】
\(x=1+\sqrt{5}i\) のとき \(x^3-3x^2+3x-1\) の値を計算せよ.
ただし、\(i\) は虚数単位である.
考え方
\(x=1+\sqrt{5}i\) を \(x^3-3x^2+3x-1\) に素直に代入すると、
\(x^3-3x^2+3x-1\\=(1+\sqrt{5}i)^3-3(1+\sqrt{5}i)^2+3(1+\sqrt{5}i)-1 \)
この計算を頑張れば答えは出ますが・・・。
時として、このような計算力も必要ですので、是非一度は頑張ってやってほしいものですが・・・。
ここでは計算の工夫を行うことで、できるだけ簡単・計算ミスなく処理をするかについてお話をしていきます。
数学ができる人とそうでない人は、ただの計算1つをとっても差がつきます。
ただの計算と侮ることなく、しっかりと計算のテクニックを身につけましょう!
解法1(今回の問題のみ有効)
\(x^3-3x^2+3x-1\) の式をじ~っと見て見て下さい!
何か見えてきませんか??
これは有名な公式ですよね??
\(x^3-3x^2+3x-1=(x-1)^3\) !!
※\((a-b)^3=a^3-3a^2b+3ab^2-b^3\) を利用
よって因数分解した形に \(x=1+\sqrt{5}i\) を代入すると、
\(x^3-3x^2+3x-1=(x-1)^3=(\sqrt{5}i)^3=-5\sqrt{5}i\)
この問題に限って言えば、この解法が最も簡単かつ早く処理できます。
しかし、多くの問題でここまで都合よく計算できるわけではありません。
一般的(どのような数字でも)にただ代入するよりは早く処理できる解法を以下で紹介します。
解法2(幅広く使える解法)
\(x=1+\sqrt{5}i\) より
\(x-1=\sqrt{5}i\)
2 乗して
\((x-1)^2=-5\)
展開して式を整理すると
\(x^2-2x+6=0\) ・・・①
\(x^3-3x^2+3x-1\) を①の左辺で割ると
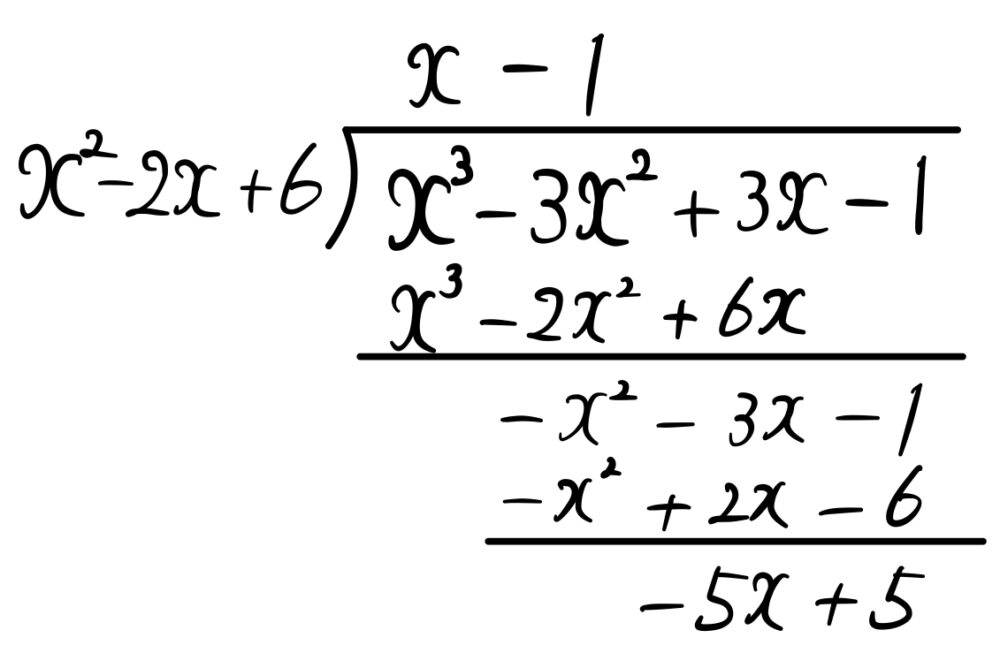
\(x^3-3x^2+3x-1=(x-1)( x^2-2x+6)-5x+5\) ・・・②
\(x=1+\sqrt{5}i\) のとき
\(x^2-2x+6=0\) であるから、
②に \(x=1+\sqrt{5}i\) を代入すると言うのは、
余りの \(-5x+5\) に \(x=1+\sqrt{5}i\) を代入すればよい
したがって求める値は、
\(-5(1+\sqrt{5}i)+5=-5\sqrt{5}i \)
最後に
解法2の計算であれば、与えられる式の次数がいくらになっても、2 次式で割った余り(1次式以下)に代入するだけであるから、計算ミスが大きく減り、時間短縮にもなる。
また、3 次関数の極値を求める際の計算など、様々な分野でもこの計算は活用できるため、是非この計算の流れは身に付けておきたい!






コメント