2021 一橋大学(第5問)｜積分・確率・整数(総合問題)

考え方

与式の $\displaystyle\int_{a-3}^{a+3} (x-b)(x-c) \enspace dx$ をそのまま計算しても良いが、もの凄く煩雑な計算、そして文字が複数登場し、大変であることが容易に想像できます。

だからこそ、何かしらの工夫を施したいと考えられるようになって欲しい！(最初からゴリ押しの計算はやめましょう！ゴリ押しの計算は最終手段！！)

そこで、積分区間に注目し、以下の

Ⅰ．平行移動

Ⅱ．偶関数・奇関数の利用

を上手に活用しましょう！

Ⅰ．平行移動

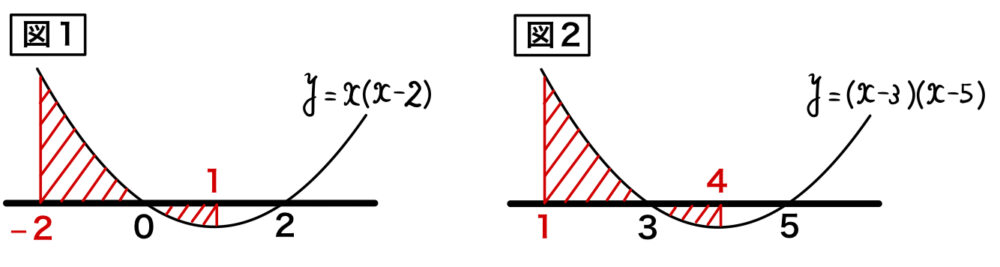
図２は、図１を $x$ 軸方向に $3$ 平行移動しただけであるから、

$\displaystyle\int_{-2}^{1} x(x-2) \enspace dx = \displaystyle\int_{-2+3}^{1+3} (x-3)(x-2-3) \enspace dx = \displaystyle\int_{1}^{4} (x-3)(x-5) \enspace dx$

が成立する

つまり

$\displaystyle\int_{a-3}^{a+3} (x-b)(x-c) \enspace dx$

を $x$ 軸方向に $-a$ 平行移動して

$\displaystyle\int_{a-3}^{a+3} (x-b)(x-c) \enspace dx=\displaystyle\int_{ -3}^{ +3} (x+a-b)(x+a-c) \enspace dx$ と変形できる

Ⅱ．偶関数・奇関数の利用

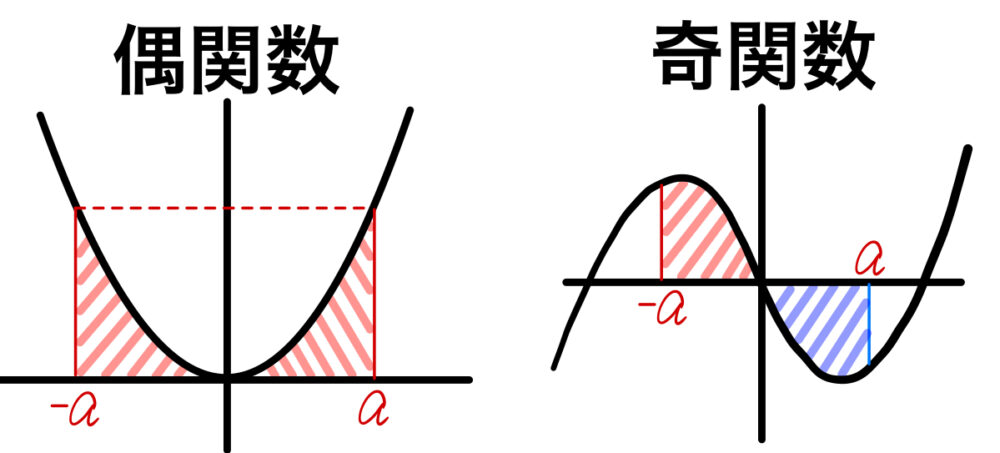
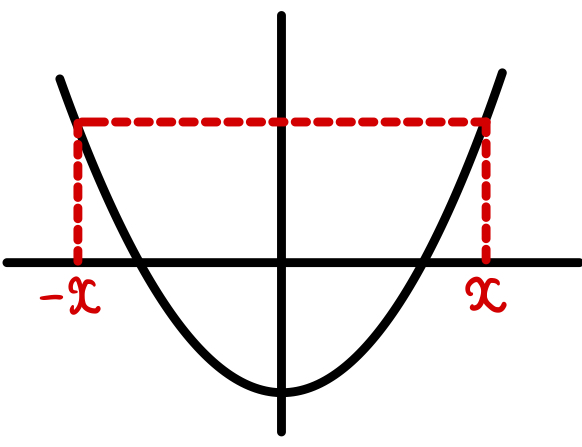
$y=f(x)$ が偶関数のとき

$\displaystyle\int_{-a}^{a} f(x) \enspace dx = 2\displaystyle\int_{0}^{a} f(x) \enspace dx$

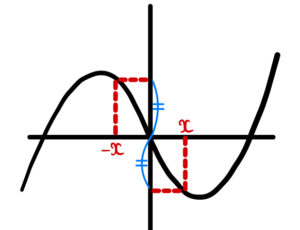
$y=f(x)$ が奇関数のとき

$\displaystyle\int_{-a}^{a} f(x) \enspace dx = 0$

解答

$\displaystyle\int_{a-3}^{a+3} (x-b)(x-c) \enspace dx=I$ とおく．

$b≦c$ のとき

【考え方　Ⅰ．平行移動】の考え方を利用して

$I = \displaystyle\int_{ -3}^{ +3} (x+a-b)(x+a-c) \enspace dx$ とおける．

ここで、$\alpha=b-a$、$\beta=c-a$ とおく．

$1≦a≦6$、$1≦b≦c≦6$ より $-5≦\alpha≦\beta≦5$

$I = \displaystyle\int_{ -3}^{ +3} (x-\alpha)(x-\beta) \enspace dx\\ = \displaystyle\int_{ -3}^{ +3} \left\{ x^2-(\alpha+\beta)x+\alpha\beta\right\} \enspace dx$

【考え方　Ⅱ．偶関数・奇関数の利用】の考え方を利用して

$I = 2\displaystyle\int_{ 0 }^{ +3} (x^2+\alpha\beta) \enspace dx \\ = 2\left[\displaystyle\frac{1}{3}x^3+\alpha\beta x \right]^{3}_{0}\\ = 18+6\alpha\beta$

$I=0$ より

$18+6\alpha\beta = 0$

$\alpha\beta = -3$

$-5≦\alpha≦\beta≦5$ より

$( \alpha , \beta ) = ( -1 , 3 ) , ( -3 , 1 )$

つまり、$( b-a , c-a ) = ( -1 , 3 ) , ( -3 , 1 )$

これを満たす $( a , b , c )$ を計算すると

$( a , b , c ) = ( 2 , 1 , 5 ) , ( 3 , 2 , 6 ) , ( 4 , 1 , 5 ) , ( 5 , 2 , 6 )$ の $4$ 通り

$b>c$ のとき、同様に考えて

$( a , b , c ) = ( 2 , 5 , 1 ) , ( 3 , 6 , 2 ) , ( 4 , 5 , 1 ) , ( 5 , 6 , 2 )$ の $4$ 通り

以上より求める確率は、$\displaystyle\frac{8}{6^3}= \displaystyle\frac{1}{27}$