【2008お茶の水女子大学】
\(a\)、\(b\)、\(c\)、\(d\) を正の整数とし、\(\displaystyle\frac{c}{d}<\displaystyle\frac{a}{b}\) とする.
このとき、\(\displaystyle\frac{c}{d}<\displaystyle\frac{a+c}{b+d}<\displaystyle\frac{a}{b}\) が成り立つことを示せ.
式の意味を理解しよう
『 \(A>B\) を示せ』という不等式の証明の王道の解法は、
\(A-B\) を計算して、これが正 ( \(A-B>0\) ) であることを示す.
もちろんそのような王道の解法も1つである.
しかしここでは、ただただ証明できて終わりではなく、この不等式が何を意味するのか、多角的に式の意味を考え、小学生でもわかる証明(説明)方法を3つ紹介します。
解法①は、王道の差をとって正になることの証明
解法②は、図形的なアプローチ
解法③は、小学生に説明する方法
の3つの解答です。
解法①差が正になることの証明
\(a\)、\(b\)、\(c\)、\(d\) を正の整数とし、\(\displaystyle\frac{c}{d}<\displaystyle\frac{a}{b}\) より
\(ad-bc>0\) ・・・①
\(\displaystyle\frac{a+c}{b+d}-\displaystyle\frac{c}{d}=\displaystyle\frac{ad-bc}{(b+d)d}\)
①より、\(\displaystyle\frac{ad-bc}{(b+d)d}>0\) であるから、
\(\displaystyle\frac{a+c}{b+d}>\displaystyle\frac{c}{d}\)
次に、
\(\displaystyle\frac{a}{b}-\displaystyle\frac{a+c}{b+d}=\displaystyle\frac{ad-bc}{b(b+d)}\)
①より、\(\displaystyle\frac{ad-bc}{b(b+d)}>0\) であるから、
\(\displaystyle\frac{a}{b}>\displaystyle\frac{a+c}{b+d}\)
したがって題意は示された.
解法②図形的なアプローチ
\(2\) 直線の傾きに注目する.下図より、
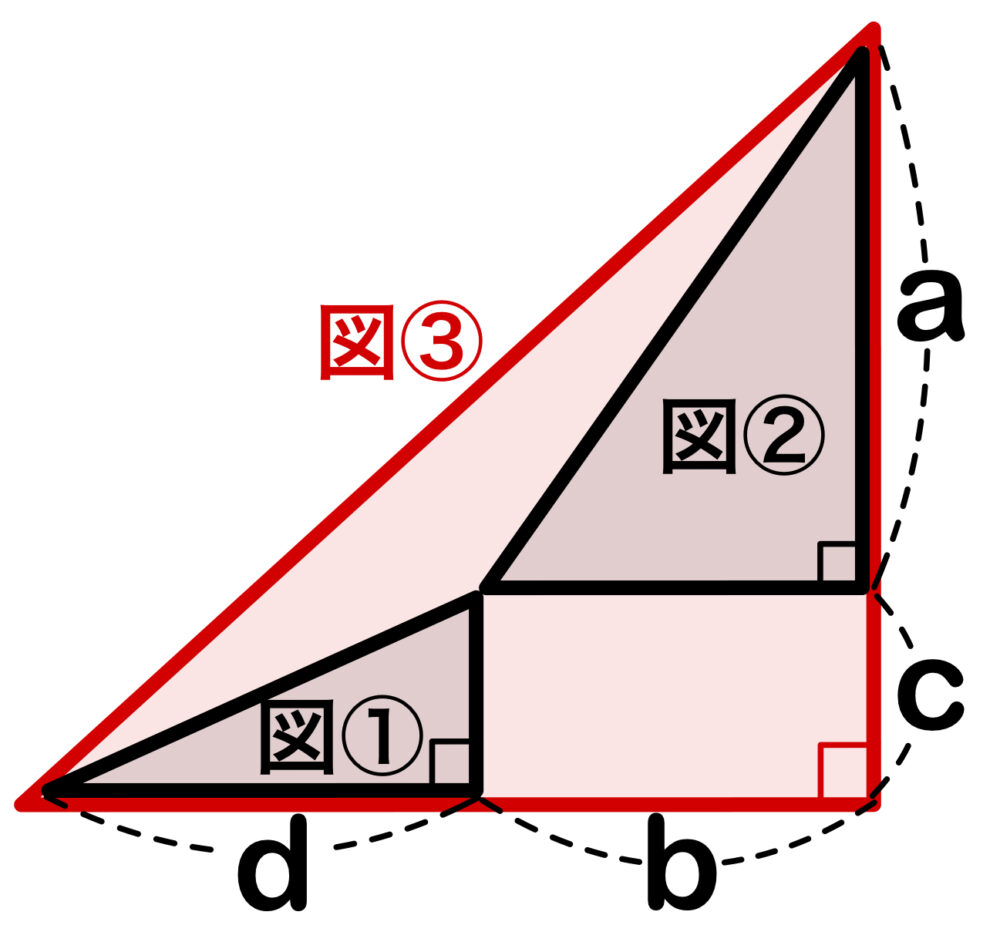
図①の三角形の傾きは \(\displaystyle\frac{c}{d}\)、図②の三角形の傾きは \(\displaystyle\frac{a}{b}\)
図③の三角形の傾きは \(\displaystyle\frac{a+c}{b+d}\) であるから、図①〜③より
\(\displaystyle\frac{c}{d}<\displaystyle\frac{a+c}{b+d}<\displaystyle\frac{a}{b}\) が成り立つ
解法③小学生に説明する方法

濃度が \(3\) %の食塩水 \(A\) と、濃度が \(7\) %の食塩水 \(B\) があります。
この \(2\) つの食塩水を混ぜた食塩水を \(C\) と呼ぶとき、
\(A\)、\(B\)、\(C\) を濃度が薄い順に並べてください!
この質問がほぼほぼ答えです!
当然ですが、濃度の薄い食塩水 \(A\) と濃い食塩水 \(B\) を混ぜてできた食塩水 \(C\) は、\(A\) よりは濃いが、\(B\) よりは薄い食塩水になることは小学生でもわかりますね!
つまり、濃度に注目すると \(A<C<B\) ということが成り立ちます.
本問は、これを文字で表した問題ということです。
もう少し具体的な例で話をしましょう。
例えば、\(A\) は \(3\) %の食塩水なので、\(c=3\)、\(d=100\) と考えることができます。
例えば、\(B\) は \(7\) %の食塩水なので、\(a=7\)、\(b=100\) と考えることができます。
このとき、\(C\) は \(A\) と \(B\) を合わせた食塩水なので、\(a+c=10\)、\(b+d=200\)
\(\displaystyle\frac{3}{100}<\displaystyle\frac{10}{200}=\displaystyle\frac{5}{100}<\displaystyle\frac{7}{100}\) が成り立つ
つまり、\(\displaystyle\frac{c}{d}<\displaystyle\frac{a+c}{b+d}<\displaystyle\frac{a}{b}\) が成り立つことを表しています.







コメント