2018年センター試験(数学ⅠA)第4問[整数]
(1)問題・考え方・解説
正の約数の個数・総和の公式
自然数 \(n\) の素因数分解が
\(n=p_{1}^{a_{1}}\times p_{2}^{a_{2}}\times p_{3}^{a_{3}}\times\cdots\times p_{k}^{a_{k}}\) のとき
ただし、\(p_{1}<p_{2}<\cdots<p_{k}\) を満たす素数、\(a_{1},a_{2},\cdots,a_{k},k\) は自然数
正の約数の個数
\((a_{1}+1)(a_{2}+1)\cdots(a_{k}+1)\)
正の約数の総和
\((1+p_{1}+p_{1}^2+\cdots+p_{1}^{a_{1}})(1+p_{2}+p_{2}^2+\cdots+p_{2}^{a_{2}})\cdots(1+p_{k}+p_{k}^2+\cdots+p_{k}^{a_{k}})\)
約数の個数に関する演習問題
「【2021早稲田大学・商】2021以下で、正の約数の和が奇数である数の個数」
(1)解答
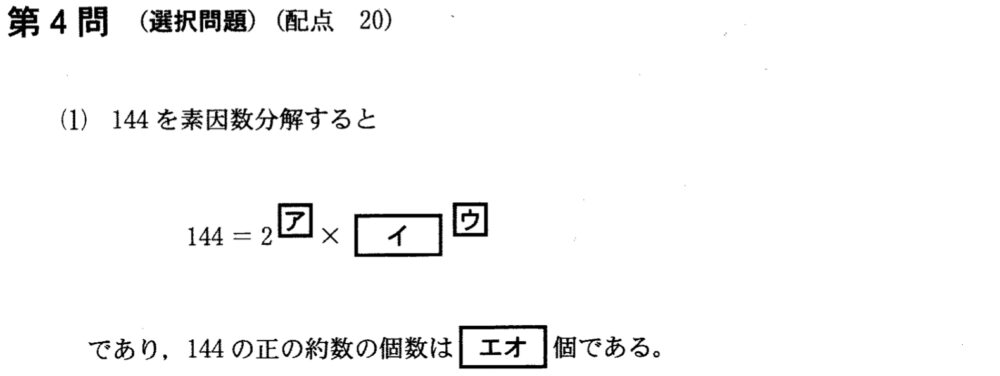
\(144=\) \(2^4\times 3^2\) ・・・〈アイウ〉より、
\(144\) の正の約数の個数は、\((4+1)(2+1)=\) \(15\) 個 ・・・〈エオ〉
(2)問題・考え方・解説
特殊解の見つけ方について
1次不定方程式の解の1つ(特殊解)の見つけ方は主に次の3つになります!
① 頑張って探す
② ユークリッドの互除法の利用
③ 合同式の利用
②については、「【頻出】1次不定方程式 (ax+by=c)の解法2つ(模範解答と時短裏技)」で紹介しています。
ここでは、「③合同式の利用」で特殊解を見つける方法を紹介します。
合同式について不安がある方は
を参考にしてください!
合同式は整数問題を扱う上で必須アイテムです!しっかりとマスターしましょう!
(2)解答・解説
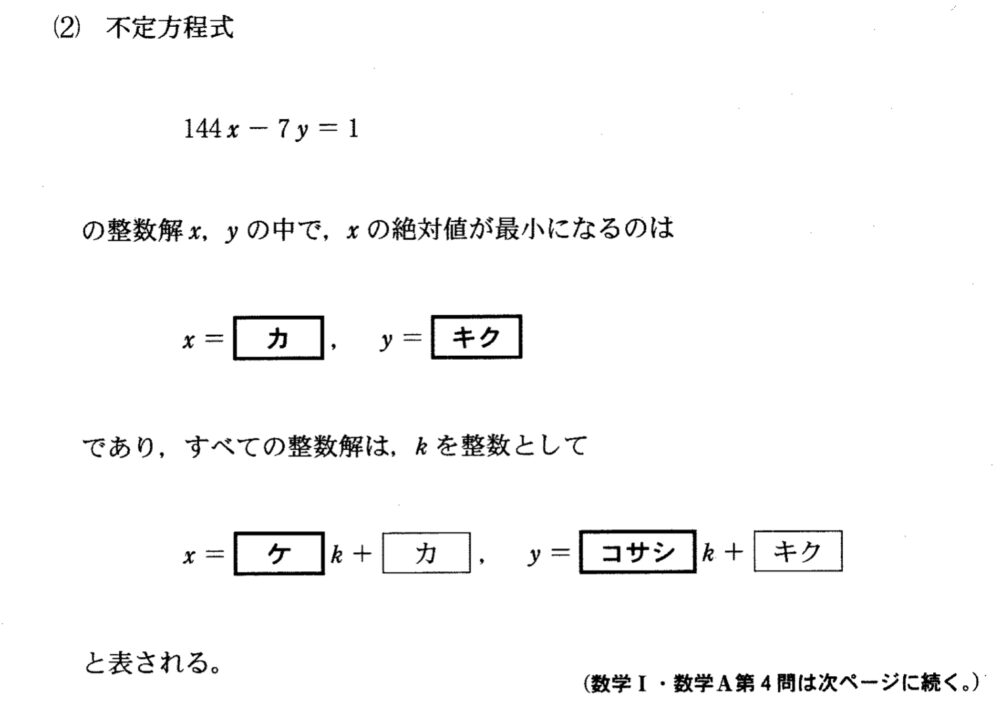
\(144x-7y=1\) ・・・① とおく
①より、\(144x=7y+1\)
以下、\( mod\) \(7\) として考えると①より
\(144x≡1\) であるから、
\(144x≡4x≡-3x\)
よって、\(4x≡1\) ・・・② かつ \(-3x≡1\) ・・・③
②+③より \(x≡2\)
このとき、\(x\) の絶対値が最小となるのは、\(x=2\) ・・・〈カ〉
①より、\(y=41\) ・・・〈キク〉
\((x,y)=(2,41)\) は①の特殊解の \(1\) つであり、①より
\(y=\displaystyle\frac{144}{7}x-\displaystyle\frac{1}{7}\)
つまり傾きが \(\displaystyle\frac{144}{7}\) であるから、傾きに注目すると
整数 \(k\) を用いて、
\(x=7k+2\) , \(y=144k+41\) ・・・〈ケ〜シ〉


(3)問題・考え方・解説

\(144\) の倍数で、\(7\) で割った余りが \(1\) となる自然数は、\(144x-7y=1\) と表せる.
(2)より、\(x=7k+2\) ・・・④ と表せる.
ここで、\(x\) が素因数に \(2\) または \(3\) 以外をもつとき、
\(144x=2^4\times 3^2\times x\) の正の約数の個数は
\((4+1)(2+1)(1+1)\)\(=30\) 個以上となるから、
\(144x=2^4\times 3^2\times x\) の正の約数が \(18\) 個のとき
\(x\) は素因数に \(2\) または \(3\) のみをもつ
最小の値を考えるので、\(x=2\) ( \(k=0\) のとき ) とすると、
\(144x=2^5\times 3^2\) となり、正の約数の個数は \((5+1)(2+1)=\) \(18\) 個となる.
したがって、\(x=2\) ・・・〈ス〉
次に、\(144x=2^4\times 3^2\times x\) の正の約数が \(30\) 個のとき
\(x\) が素因数に \(2\) または \(3\) のみをもつと仮定する.
条件を満たすためには、
- \(x=2^5=32\) のとき \(144x=2^9\times 3^2\)
- \(x=3^3=27\) のとき \(144x=2^4\times 3^5\)
- \(x=2\times 3^2=18\) のとき \(144x=2^5\times 3^4\)
のいずれかとなるが、\(x = 32 , 27 , 18\) は \(x=7k+2\) ・・・④ の形で表すことができないため不適.
したがって、④を満たし、正の約数の個数が \(30\) 個となる最小の数は、
\(k=3\) のとき、\(x=7\times 3+2=\) \(23\) ・・・〈セソ〉







コメント