【2006神戸大学・文】
平面上に原点 \(O\) から出る，相異なる \(2\) 本の半直線 \(OX\) , \(OY\) をとり，\(\angle XOY<180°\) とする．半直線 \(OX\) 上に \(O\) と異なる点 \(A\) を，半直線 \(OY\) 上に \(O\) と異なる点 \(B\) をとり，\(\overrightarrow{a}=\overrightarrow{OA}\) , \(\overrightarrow{b}=\overrightarrow{OB}\) とおく．次の問に答えよ．
(１) 点 \(C\) が \(\angle XOY\) の二等分線上にあるとき，ベクトル \(\overrightarrow{c}=\overrightarrow{OC}\) はある実数 \(t\) を用いて
\(\overrightarrow{c}=t\left(\displaystyle\frac{\overrightarrow{a}}{\left|\overrightarrow{a}\right|}+\displaystyle\frac{\overrightarrow{b}}{\left|\overrightarrow{b}\right|}\right)\)
と表されることを示せ．
(２) \(\angle XOY\) の二等分線と \(\angle XAB\) の二等分線の交点を \(P\) とおく．
\(OA=2\) , \(OB=3\) , \(AB=4\) のとき，\(\overrightarrow{p}=\overrightarrow{OP}\) を \(\overrightarrow{a}\) , \(\overrightarrow{b}\) を用いて表せ．
角の二等分線のベクトル
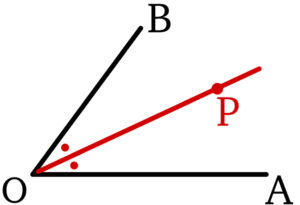一直線上にない \(3\) 点 \(O\) , \(A\) , \(B\) に対して，\(\angle AOB\) の二等分線上の点を \(P\) とするとき，実数 \(t\) を用いて
\(\overrightarrow{OP}=t\left(\displaystyle\frac{\overrightarrow{OA}}{\left|\overrightarrow{OA}\right|}+\displaystyle\frac{\overrightarrow{OB}}{\left|\overrightarrow{OB}\right|}\right)\)
※ とても有名な形です。結果は覚えておきましょう！
(１)の問題がなぜこの形になるかの証明問題になっています。ちなみにこれは数学B，４STEPの87番に発展問題としても記載されています。
単位ベクトルについて
大きさが \(1\) であるベクトルのことを単位ベクトルという．
ある \(\overrightarrow{a}\) (ただし \(\overrightarrow{0} \)ではない ) の単位ベクトルは，\(\displaystyle\frac{\overrightarrow{a}}{ \left|\overrightarrow{a}\right|} \) と表せる．
解答
(１)
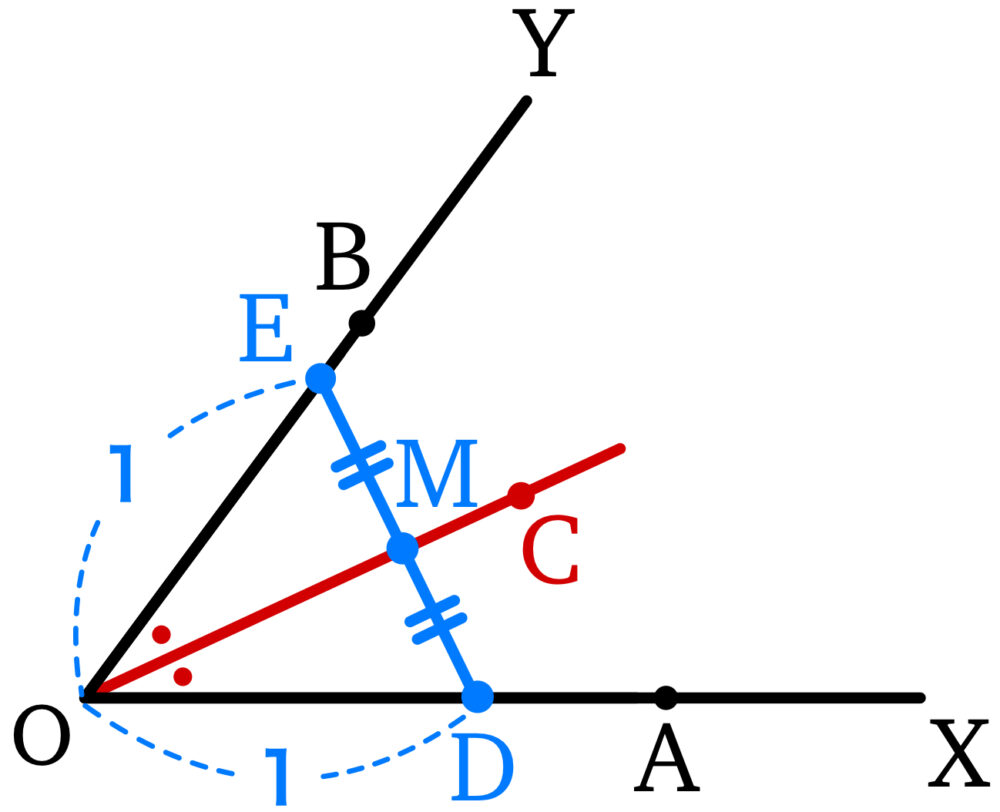\(\overrightarrow{OD}=\displaystyle\frac{\overrightarrow{OA}}{\left|\overrightarrow{OA}\right|}\) , \(\overrightarrow{OE}=\displaystyle\frac{\overrightarrow{OB}}{\left|\overrightarrow{OB}\right|}\) とおくと，\(\left|\overrightarrow{OD}\right|=\left|\overrightarrow{OE}\right|=1\) であるから，\(\triangle ODE\) は二等辺三角形である．
線分 \(DE\) の中点を \(M\) とすると，
\(\overrightarrow{OM}=\displaystyle\frac{1}{2}\left(\overrightarrow{OD}+\overrightarrow{OE}\right)=\displaystyle\frac{1}{2}\left(\displaystyle\frac{\overrightarrow{OA}}{\left|\overrightarrow{OA}\right|}+\displaystyle\frac{\overrightarrow{OB}}{\left|\overrightarrow{OB}\right|}\right)\)
また，\(\triangle ODE\) は二等辺三角形であるから，直線 \(OM\) は \(\triangle AOB\) の二等分線である．
ゆえに点 \(C\) は直線 \(OM\) 上であるから，実数 \(k\) を用いて
\(\overrightarrow{OC}=k\overrightarrow{OM}=\displaystyle\frac{k}{2}\left(\displaystyle\frac{\overrightarrow{OA}}{\left|\overrightarrow{OA}\right|}+\displaystyle\frac{\overrightarrow{OB}}{\left|\overrightarrow{OB}\right|}\right)\)
したがって，\(\overrightarrow{c}=\overrightarrow{OC}\) はある実数 \(t\) を用いて
\(\overrightarrow{c}=t\left(\displaystyle\frac{\overrightarrow{a}}{\left|\overrightarrow{a}\right|}+\displaystyle\frac{\overrightarrow{b}}{\left|\overrightarrow{b}\right|}\right)\) と表される．
(２)
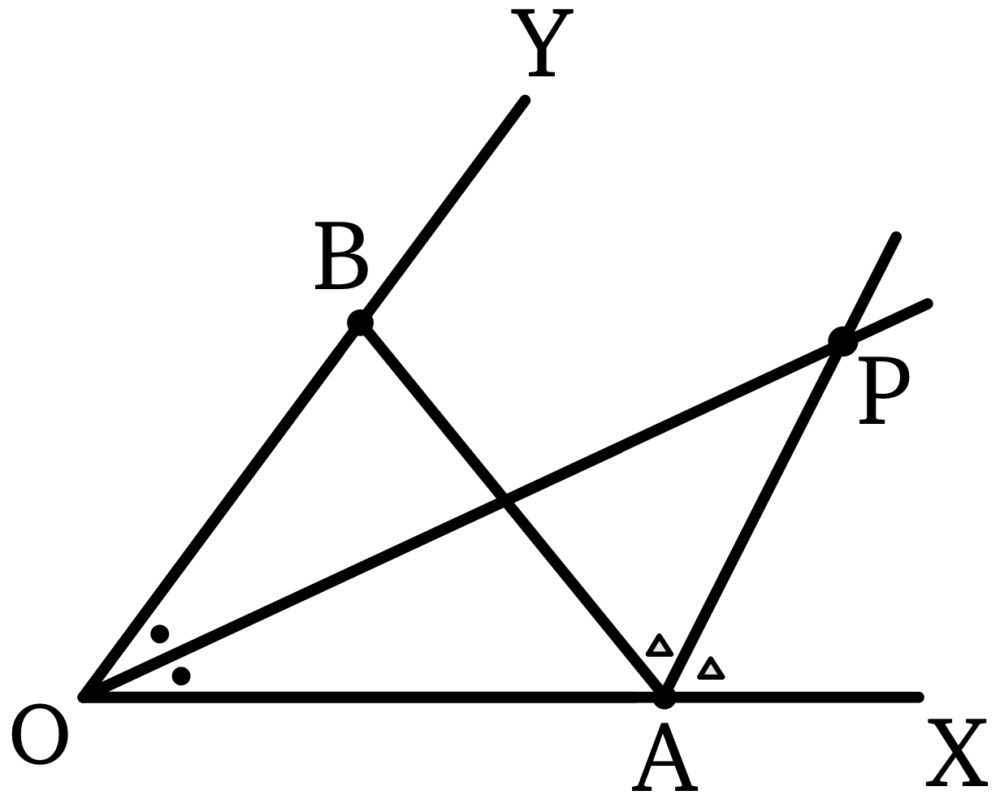
点 \(P\) は \(\triangle XOY\) の二等分線上の点なので，(１)より
\(\overrightarrow{OP}=t\left(\displaystyle\frac{\overrightarrow{a}}{\left|\overrightarrow{a}\right|}+\displaystyle\frac{\overrightarrow{b}}{\left|\overrightarrow{b}\right|}\right)\)
と表され，\(OA=2\) , \(OB=3\) であるから，
\(\overrightarrow{OP}=\displaystyle\frac{t}{2}\overrightarrow{a}+\displaystyle\frac{t}{3}\overrightarrow{b}\) ・・・①
また，点 \(P\) は \(\triangle XAB\) の二等分線上の点なので，(１)と同様に考えると，ある実数 \(s\) を用いて
\(\overrightarrow{AP}=s\left(\displaystyle\frac{\overrightarrow{OA}}{\left|\overrightarrow{OA}\right|}+\displaystyle\frac{\overrightarrow{AB}}{\left|\overrightarrow{AB}\right|}\right)\)
と表され，\(OA=2\) , \(AB=4\) であるから
\(\overrightarrow{OP}-\overrightarrow{a}=s\left(\displaystyle\frac{\overrightarrow{a}}{2}+\displaystyle\frac{\overrightarrow{b}-\overrightarrow{a}}{4}\right)\)
よって，\(\overrightarrow{OP}=\left(1+\displaystyle\frac{s}{4}\right)\overrightarrow{a}+\displaystyle\frac{s}{4}\overrightarrow{b}\) ・・・②
\(\overrightarrow{a}\) , \(\overrightarrow{b}\) は一次独立なベクトルであるから，①，②より
\(\displaystyle\frac{t}{2}=1+\displaystyle\frac{s}{4}\) かつ \(\displaystyle\frac{t}{3}=\displaystyle\frac{s}{4}\)
よって，\(t=6\) , \(s=8\)
①(または②)より，\(\overrightarrow{OP}=\overrightarrow{p}=3\overrightarrow{a}+2\overrightarrow{b}\)
コメント