【2020一橋大学】
\(x>0\) に対し,\(F(x)=\displaystyle\frac{1}{x}\displaystyle\int^{2+x}_{2-x}| t-x | dt\) と定める.
\(F(x)\) の最小値を求めよ.
解答・解説
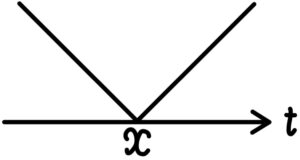 \(y=|t-x|\) のグラフは右図のようになる.
\(y=|t-x|\) のグラフは右図のようになる.
\(2-x≦t≦2+x\) における面積を考えると,
\(x<2+x\) であるから
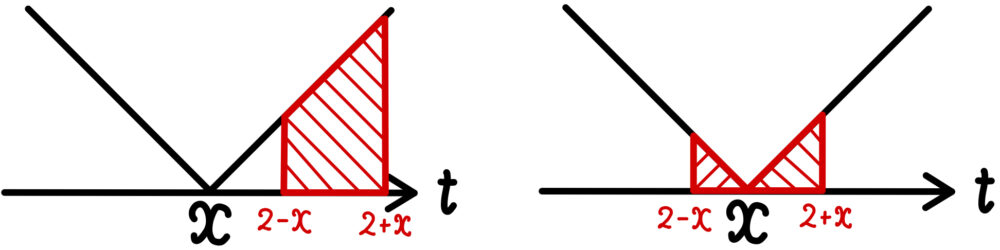
( ⅰ ) \(0<x≦2-x\) \(\iff\) \(0<x≦1\) のとき
\(F(x)=\displaystyle\frac{1}{x}\displaystyle\int^{2+x}_{2-x}(t-x) dx\)
\(=\displaystyle\frac{1}{x}\Bigl[\displaystyle\frac{1}{2}t^2-xt\Bigr]^{2+x}_{2-x}\)
\(=-2x+4\)
\(F(x)=-2x+4\) は減少関数であるから,\(x=1\) で最小値 \(2\) をとる.
( ⅱ ) \(2-x<x\) \(\iff\) \(x>1\) のとき
\(F(x)=\displaystyle\frac{1}{x}\displaystyle\int^{x}_{2-x}-(t-x) dx+\displaystyle\frac{1}{x}\displaystyle\int^{2+x}_{x}(t-x) dx\)
\(=\displaystyle\frac{1}{x}\left\{\displaystyle\frac{1}{2}(2x-2)^2+\displaystyle\frac{1}{2}\cdot 2^2\right\}\)
\(=2x+\displaystyle\frac{4}{x}-4\)

逆数の和の最小値を考える問題ですから,相加平均・相乗平均の関係を利用することができます!
相加・相乗平均の関係については、「相加平均・相乗平均の関係はいつ使う?使うタイミングの見抜き方(基本)」を参考に!
\(2x>0\) , \(\displaystyle\frac{4}{x}>0\) であるから相加平均・相乗平均の関係より
\(2x+\displaystyle\frac{4}{x}≧2\sqrt{2x\cdot\displaystyle\frac{4}{x}}=4\sqrt{2}\)
よって,\(F(x)=2x+\displaystyle\frac{4}{x}-4≧4\sqrt{2}-4\)
等号成立は,\(2x=\displaystyle\frac{4}{x}\) \(\iff\) \(x^2=2\)
\(x>1\) より \(x=\sqrt{2}\) のとき \(F(x)\) は最小値 \(4\sqrt{2}-4\) をとる
ここで,\(4\sqrt{2}=\sqrt{32}<\sqrt{36}=6\) より
\(4\sqrt{2}-4<2\) となる.
したがって( ⅰ ),( ⅱ )より
\(F(x)\) は \(x=\sqrt{2}\) で最小値 \(4\sqrt{2}-4\)








コメント