【2022数学ⅡB】第2問(微分法・積分法)
[1](1)問題と解答・解説《ア〜イ》
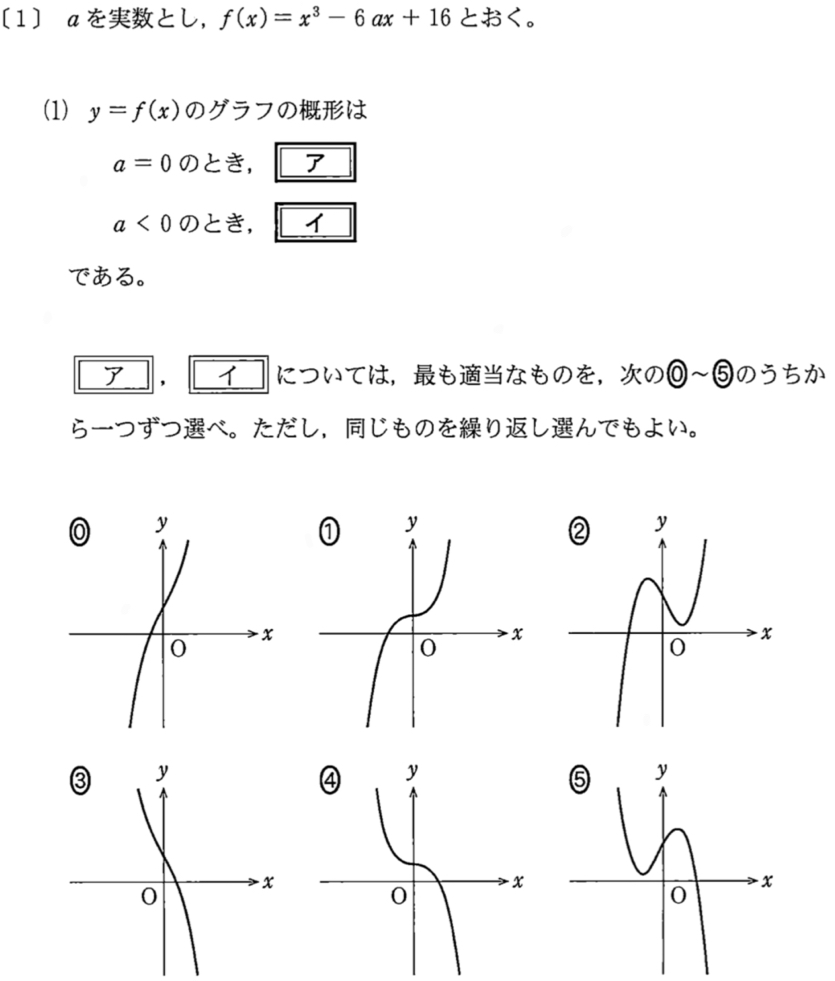
解答・解説《ア〜イ》
\(f(x)=x^3-6ax+16\) より
\(f^{\prime}(x)=3x^2-6a\)
・\(a=0\) のとき
\(f^{\prime}(x)=3x^2≧0\) となり
\(x=0\) のときのみ \(f^{\prime}(x)=0\)
よって,\((0,16)\) で接線の傾きが \(0\) となり,
\(y=f(x)\) は単調増加なグラフとなる.
よって,① ・・・《ア》
・\(a<0\) のとき
\(-6a>0\) より,\(f^{\prime}(x)=3x^2-6a>0\)
よって \(y=f(x)\) は単調増加なグラフとなるので,⓪ ・・・《イ》
[1](1)(2)問題と解答・解説《ウ〜コ》

解答・解説《ウ〜コ》
(2) \(a>0\) のとき
\(f^{\prime}(x)=3(x^2-2a)\) なので
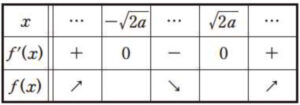 \(f^{\prime}(x)=0\) \(\iff\) \(x=\pm\sqrt{2a}\)
\(f^{\prime}(x)=0\) \(\iff\) \(x=\pm\sqrt{2a}\)
よって増減表は右のようになり,
\(f\left(-\sqrt{2a}\right)=\left(-\sqrt{2a}\right)^3-6a(-\sqrt{2a})+16=4\sqrt{2}a^{\frac{3}{2}}+16\)
\(f\left(\sqrt{2a}\right)=\left(\sqrt{2a}\right)^3-6a\sqrt{2a}+16=-4\sqrt{2}a^{\frac{3}{2}}+16\)
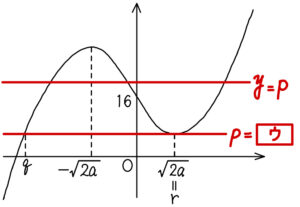 であるから,\(y=f(x)\) のグラフは右図のようになる.
であるから,\(y=f(x)\) のグラフは右図のようになる.
\(y=p\) が \(3\) 個の共有点をもつとき
\(-4\sqrt{2}a^{\frac{3}{2}}+16<p<4\sqrt{2}a^{\frac{3}{2}}+16\) ・・・《ウ:③,エ:②》
\(p=-4\sqrt{2}a^{\frac{3}{2}}+16\) のとき
\(y=f(x)\) と \(y=p\) は \(2\) 個の共有点をもち,\(r=\sqrt{2a}\)

\(q\) の座標の求め方については,共通テストで使える変曲点を利用した裏技!
『(交点〜変曲点):(変曲点〜接点)=2:1』
の性質を利用して処理します。
変曲点についての裏技性質は⏬を参考に!

\(f(x)=x^3-6ax+16\) より
\(f^{\prime}(x)=3x^2-6a\)
\(f^{\prime\prime}(x)=6x\)
\(f^{\prime\prime}(x)=0\) より \(x=0\) (←変曲点の \(x\) 座標)
接点は \(x=r=\sqrt{2a}\) であるから,
『(交点〜変曲点):(変曲点〜接点)=2:1』の性質を利用すると
交点の \(x\) 座標は \(x=q=-2\sqrt{2a}\)
したがって,\(q=-2\sqrt{2}a^{\frac{1}{2}}\) , \(r=\sqrt{2}a^{\frac{1}{2}}\) ・・・《オ〜ク》
(3) 方程式 \(f(x)=0\) の異なる実数解の個数 \(n\) は,(1)より
\(a<0\) ならば \(n=1\) ・・・《ケ:①》
また,\(n=3\) となるのは \(a>0\) のときであるから,\(n=3\) ならば \(a>0\) ・・・《コ:④》
[2]問題と解答・解説《サ〜ノ》
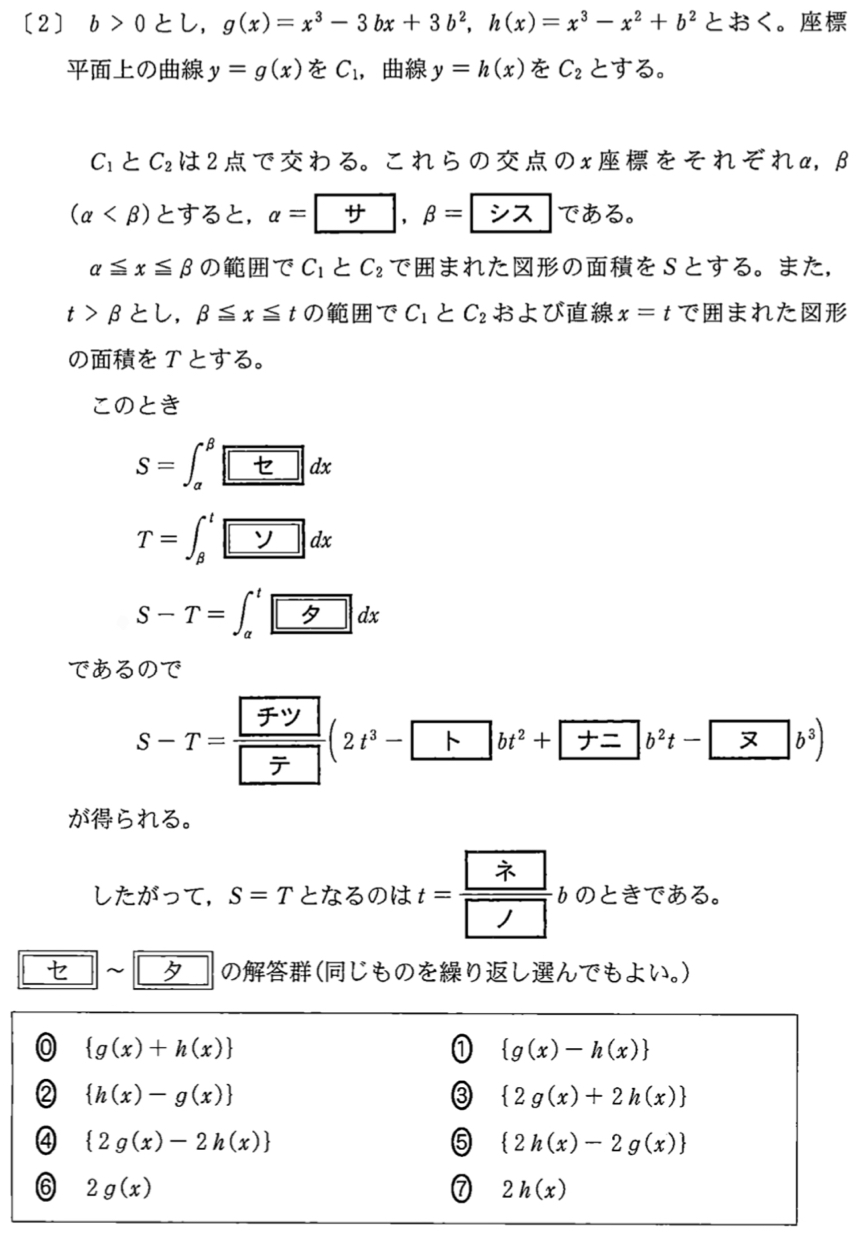
解答・解説《サ〜ノ》
\(g(x)=h(x)\) のとき
\(g(x)-h(x)=(x^3-bx+3b^2)-(x^3-x^2+b^2)\)
\(=x^2-3bx+2b^2\)
\(=(x-b)(x-2b)\) より
\(C_{1}\) , \(C_{2}\) の交点は,\((x-b)(x-2b)=0\)
\(x= b , 2b\)
\(b>0\) , \(\alpha≦x≦\beta\) より,
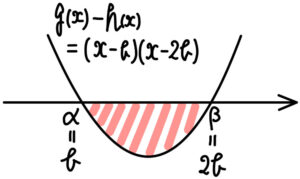 \(\alpha=b\) , \(\beta=2b\) ・・・《サ〜ス》
\(\alpha=b\) , \(\beta=2b\) ・・・《サ〜ス》
\(\alpha≦x≦\beta\) において
\(g(x)-h(x)≦0\)
つまり \(g(x)≦h(x)\) であるから
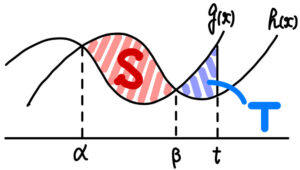 \(y=g(x)\) と \(y=h(x)\) のグラフの概形の位置関係は右図のような位置関係になる.
\(y=g(x)\) と \(y=h(x)\) のグラフの概形の位置関係は右図のような位置関係になる.
よって,
\(S=\displaystyle\int^{\beta}_{\alpha}\left\{h(x)-g(x)\right\} dx\) ・・・《セ:②》
\(T=\displaystyle\int^{t}_{\beta}\left\{g(x)-h(x)\right\} dx\) ・・・《ソ:①》
であるから,
\(S-T=\displaystyle\int^{\beta}_{\alpha}\left\{h(x)-g(x)\right\} dx-\displaystyle\int^{t}_{\beta}\left\{g(x)-h(x)\right\} dx\)
\(=\displaystyle\int^{\beta}_{\alpha}\left\{h(x)-g(x)\right\} dx+\displaystyle\int^{t}_{\beta}\left\{h(x)-g(x)\right\} dx\)
\(=\displaystyle\int^{t}_{\alpha}\left\{h(x)-g(x)\right\} dx\) ・・・《タ:②》
よって,
\(S-T=\displaystyle\int^{t}_{b}(-x^2+3bx-2b^2) dx\)
\(=\Bigl[-\displaystyle\frac{1}{3}x^3+\displaystyle\frac{3}{2}bx^2-2b^2x\Bigr]^{t}_{b}\)
\(=\displaystyle\frac{-1}{6}(2t^3-9bt^2+12b^2t-5b^3)\) ・・・《チ〜ヌ》
\(S=T\) \(\iff\) \(S-T=0\) のとき
\(-\displaystyle\frac{1}{6}(2t^3-9bt^2+12b^2t-5b^3)=0\)
\(-\displaystyle\frac{1}{6}(2t-5b)(t-b)^2=0\) であり
\(\alpha=b<t\) より,\(t=\displaystyle\frac{5}{2}b\) ・・・《ネノ》









コメント