【2022大阪医科薬科大学・看護・[4]】
解答・解説
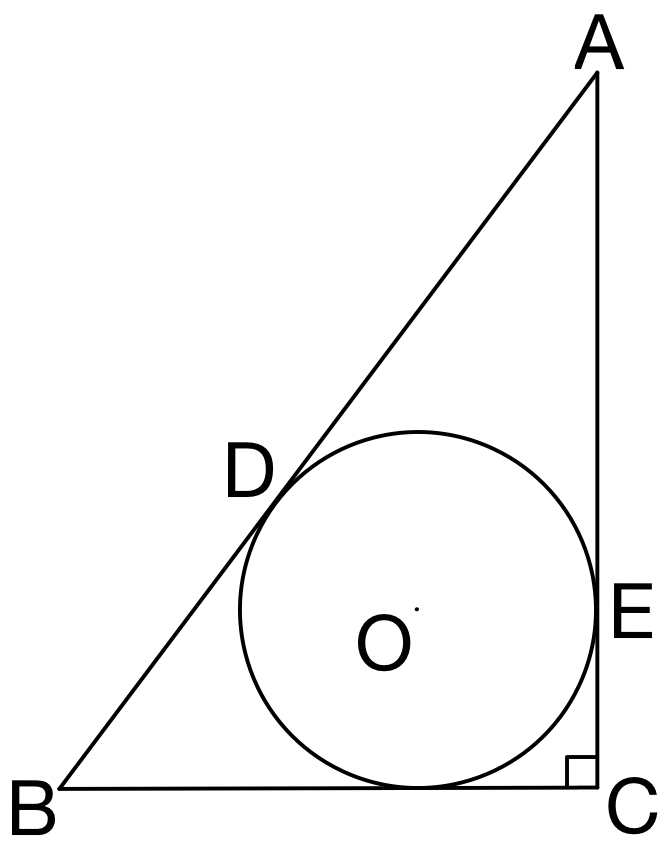
(１) 内接円の半径
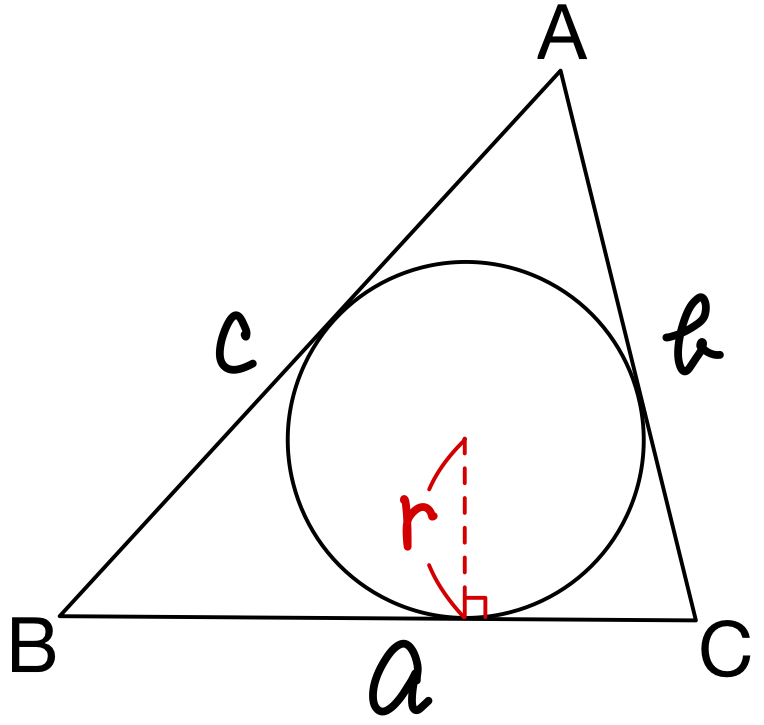内接円の半径
三角形 \(ABC\) の 内接円の半径を \(r\) ，面積を \(S\) とすると，
\(S=\displaystyle\frac{1}{2}r(a+b+c)\)
\(AB^2=BC^2+CA^2\) が成立するので，
\(\triangle ABC\) は \(\angle C=90°\) となる直角三角形
よって，\(\triangle ABC=\displaystyle\frac{1}{2}\times BC\times AC=\displaystyle\frac{1}{2}\times 6\times 8=24\)
したがって，\(24=\displaystyle\frac{1}{2}r(10+6+8)\)
\(\iff\) \(r=2\) ・・・( e )
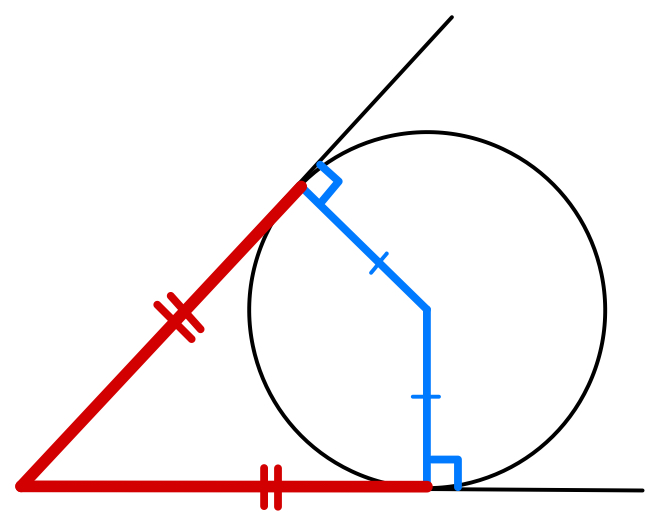(２) 円の接線
円の接線
円の外部の \(1\) 点からその円に引いた \(2\) 本の接線について，
\(2\) つの接線の長さは等しい
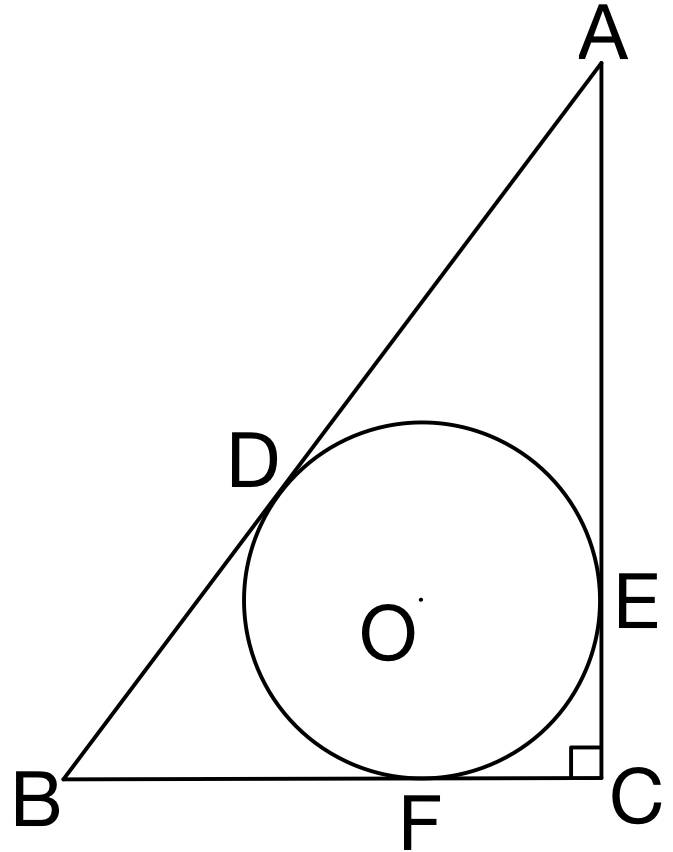
円 \(O\) と線分 \(BC\) の接点を \(F\) とおく．
円の接線の性質より \(AD=AE\)，\(BD=BF\)，\(CE=CF\)
ここで \(AD=AE=x\) とおくと
\(BD=BF=10-x\)，\(CE=CF=8-x\)
\(BC=BF+CF=(10-x)+(8-x)=6\) より
\(x=AD=6\) ・・・( a )
(３) 合同、接弦定理
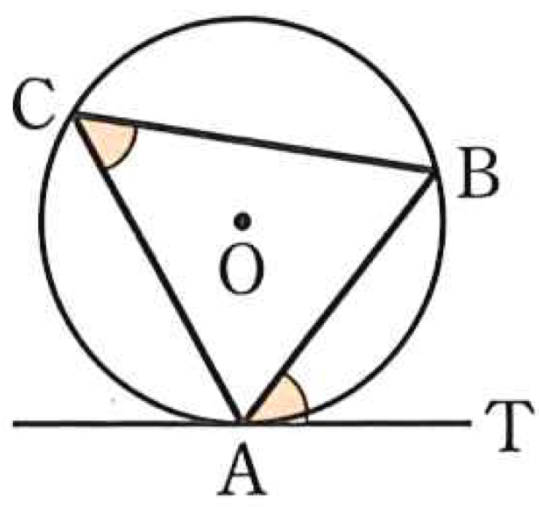接線と弦の作る角(接弦定理)
円 \(O\) の弦 \(AB\) と，その端点 \(A\) における
接線 \(AT\) が作る角 \(\angle BAT\) は，
その角の内部に含まれる孤 \(AB\) に対する円周角 \(\angle ACB\) に等しい．
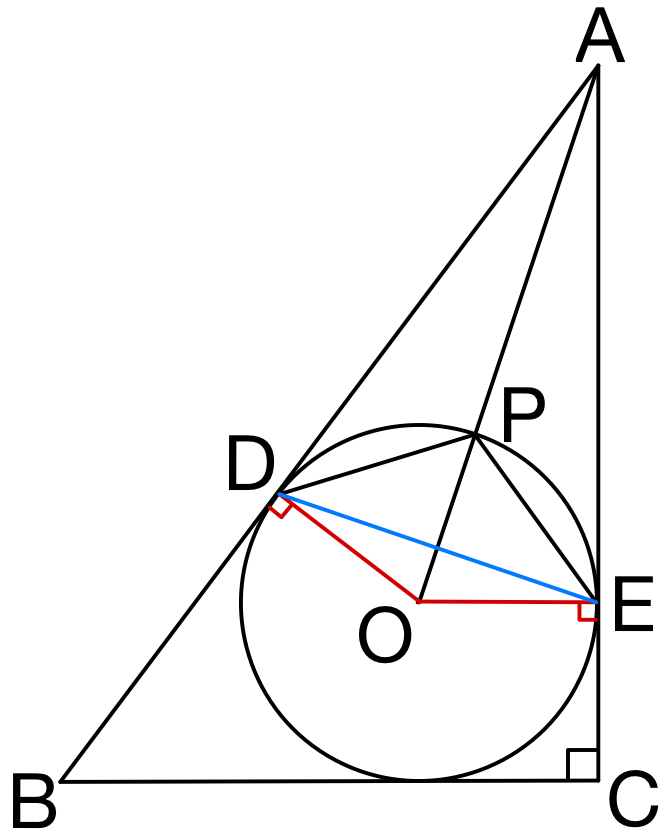
\(\triangle AOD\) と \(\triangle AOE\) について
\(AO\) は共通，\(AD=AE\)，\(\angle ADO=\angle AEO=90°\) より
\(\triangle AOD≡\triangle AOE\)
また点 \(P\) は \(AO\) 上より，
\(\angle ADP=\angle AEP\) ・・・①
次に，接弦定理より\(\angle AEP=\angle PDE\) ・・・②
①，②より，\(\angle ADP=\angle PDE\) ・・・( b )
(４)
(３)の結果から，線分 \(DP\) は \(\angle ADE\) の二等分線．
また，\(\triangle AOD≡\triangle AOE\) より
線分 \(AO\) は \(\angle DAE\) の二等分線．
よって点 \(P\) は，\(\triangle ADE\) の内接円の中心となる．
つまり，\(OI=OP=2\) ( \(\triangle ABC\) の内接円の半径 )
よって，\(OI=2\) ・・・( e )
コメント