【2022奈良女子大学・理】立方体の8個の頂点から3個選んでできる三角形について

解答・解説

(１)　三角形は全部で何個できるか．

どの頂点を \(3\) 個選んでも，その \(3\) 点はいずれも一直線上にはない．

よって，立方体の \(8\) 個の頂点から異なる \(3\) 個を選べばよい．

\(_{8}C_{3}=\displaystyle\frac{8\cdot 7\cdot 6}{3\cdot 2\cdot 1}=56\) 個

(２)　直角三角形は全部で何個できるか．

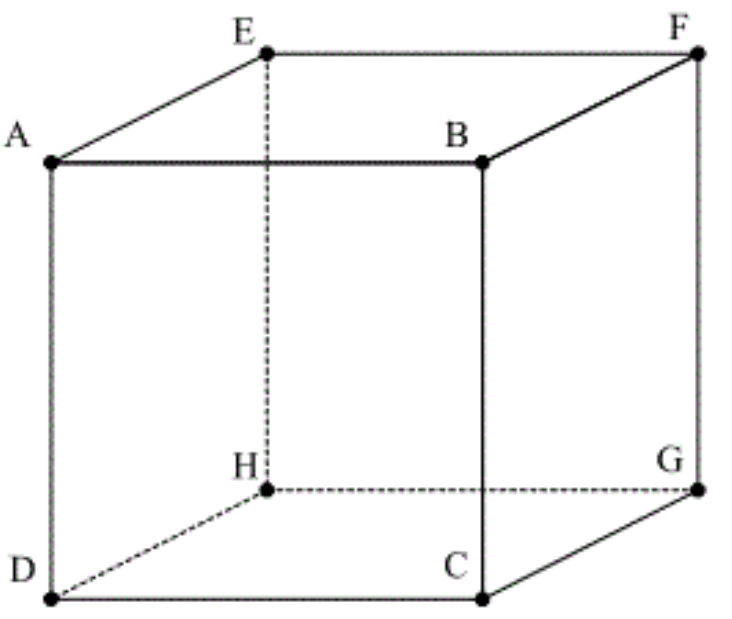
右図のように，立方体の頂点を \(A\)，\(B\)，\(C\)，\(D\)，\(E\)，\(F\)，\(G\)，\(H\) とおく．

(１)で求めた \(56\) 個の三角形はいずれも，

\(\triangle ABC\) (直角二等辺三角形) ，\(\triangle ABG\) (直角三角形) ，\(\triangle ACF\) (正三角形) のいずれかと合同となる．

( ⅰ )　\(\triangle ABC\) と合同な三角形について

\(6\) 個の面それぞれに \(4\) 個ずつできるので，

\(6\times 4=24\) 個

( ⅱ )　\(\triangle ABG\) と合同な三角形について

一辺を立方体の一辺と共有しているので，\(12\) 個の辺それぞれにおいて \(2\) 個ずつできるから

\(12\times 2=24\) 個

したがって直角三角形は，\(24+24=48\) 個

(３)　面積が \(\displaystyle\frac{7}{10}\) 以上である三角形は全部で何個できるか．

( ⅰ )　\(\triangle ABC\) と合同な三角形について

\(\triangle ABC=\displaystyle\frac{1}{2}\cdot 1\cdot 1=\displaystyle\frac{1}{2}<\displaystyle\frac{7}{10}\)

よって不適．

( ⅱ )　\(\triangle ABG\) と合同な三角形について

\(\triangle ABG=\displaystyle\frac{1}{2}\cdot 1\cdot \sqrt{2}=\displaystyle\frac{\sqrt{2}}{2}\)

ここで，\(\displaystyle\frac{\sqrt{2}}{2}=\displaystyle\frac{\sqrt{50}}{10}>\displaystyle\frac{\sqrt{49}}{10}=\displaystyle\frac{7}{10}\) より条件に適する．

( ⅲ )　\(\triangle ACF\) と合同な三角形について

\(\triangle ACF=\displaystyle\frac{1}{2}\cdot \sqrt{2}\cdot \sqrt{2}\cdot\sin \displaystyle\frac{\pi}{3}=\displaystyle\frac{\sqrt{3}}{2}\)

ここで，\(\displaystyle\frac{\sqrt{3}}{2}=\displaystyle\frac{\sqrt{75}}{10}>\displaystyle\frac{\sqrt{49}}{10}=\displaystyle\frac{7}{10}\) より条件に適する．

( ⅰ )〜( ⅲ ) より

\(\triangle ABG\)，\(\triangle ACF\) と合同な三角形の個数を求めれば良い．

(１)，(２)の結果から，\(56-24=32\) 個