【2023同志社大学・全学部日程・文系・第2問】
\(m\) を実数の定数とする.\(3\) 次方程式 \(2x^3+3x^2-12x-6m=0\) は,相異なる \(3\) つの実数解 \(\alpha\),\(\beta\),\(\gamma\) をもつとする.ただし,\(\alpha<\beta<\gamma\) とする.
(1) \(3\) 次関数 \(y=\displaystyle\frac{1}{6}(2x^3+3x^2-12x)\) の極大値と極小値をそれぞれ求めよ.
(2) \(xy\) 平面上において,\(3\) 次関数 \(y=\displaystyle\frac{1}{6}(2x^3+3x^2-12x)\) のグラフの概形を描け.
(3) \(m\) のとりうる値の範囲を求めよ.
(4) \(\gamma\) のとりうる値の範囲を求めよ.
解答・解説
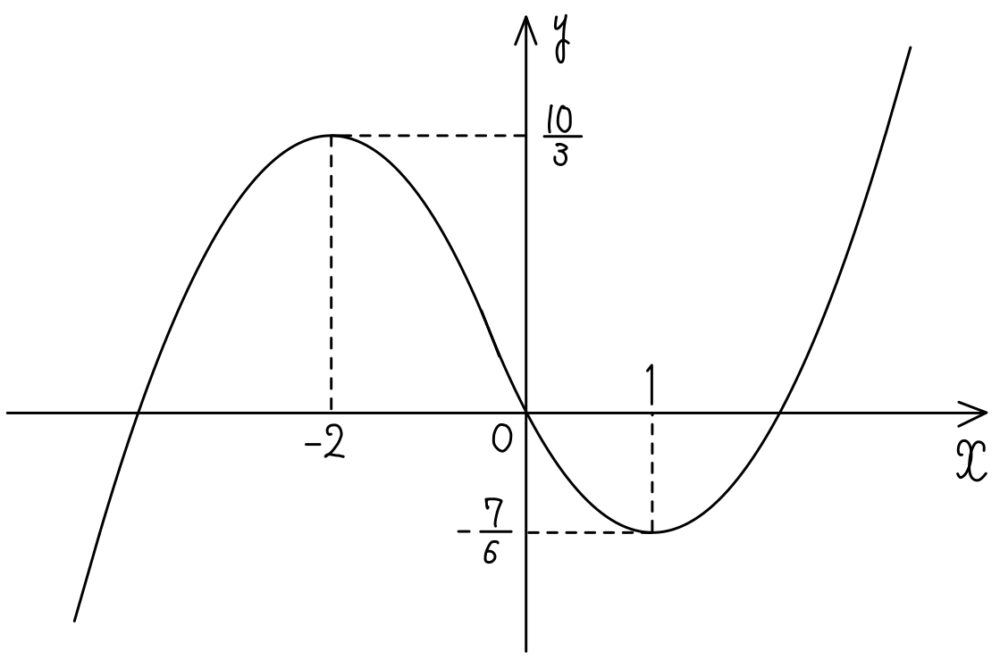
(1) \(y=\displaystyle\frac{1}{6}(2x^3+3x^2-12x)\) の極大値と極小値
\(y=\displaystyle\frac{1}{6}(2x^3+3x^2-12x)\) より
\(y^{\prime}=x^2+x-2=(x+2)(x-1)\)
\(y^{\prime}=0\) のとき \(x=-2,1\)
| \(x\) | ・・・ | \(-2\) | ・・・ | \(1\) | ・・・ |
| \(y^{\prime}\) | + | \(0\) | ー | \(0\) | + |
| \(y\) | ↗️ | ↘️ | ↗️ |
\(x=-2\) のとき極大値:\(\displaystyle\frac{10}{3}\)
\(x=1\) のとき極小値:\(-\displaystyle\frac{7}{6}\)
(2) \(y=\displaystyle\frac{1}{6}(2x^3+3x^2-12x)\) のグラフの概形
(3) \(m\) のとりうる値の範囲
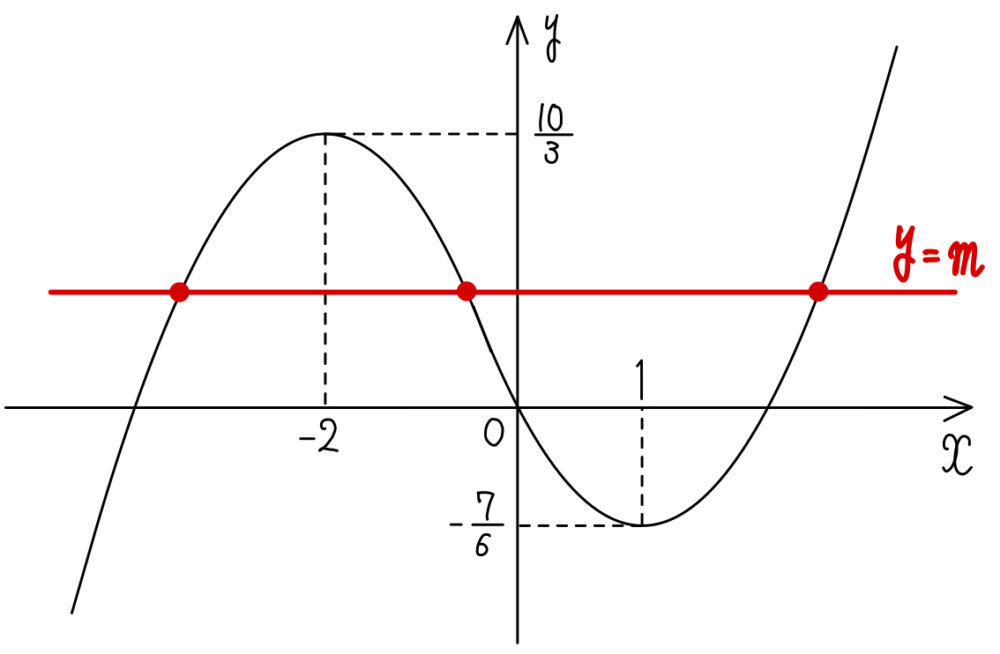
\(2x^3+3x^2-12x-6m=0\) ・・・①
\(\iff\) \(m=\displaystyle\frac{1}{6}(2x^3+3x^2-12x)\)
①の解は \(y=m\) と \(y=\displaystyle\frac{1}{6}(2x^3+3x^2-12x)\) の交点の \(x\) 座標と一致するので
(2)のグラフから相異なる \(3\) つの実数解 \(\alpha\),\(\beta\),\(\gamma\) をもつのは
\(-\displaystyle\frac{7}{6}<m<\displaystyle\frac{10}{3}\)
(4) \(\gamma\) のとりうる値の範囲
\(y=\displaystyle\frac{10}{3}\) のとき
\(\displaystyle\frac{1}{6}(2x^3+3x^2-12x)=\displaystyle\frac{10}{3}\)
\(\iff\) \(2x^3+3x^2-12x-20=0\)
\(\iff\) \((x+2)^2(2x-5)=0\)
よって,\(x=-2,-\displaystyle\frac{5}{2}\)
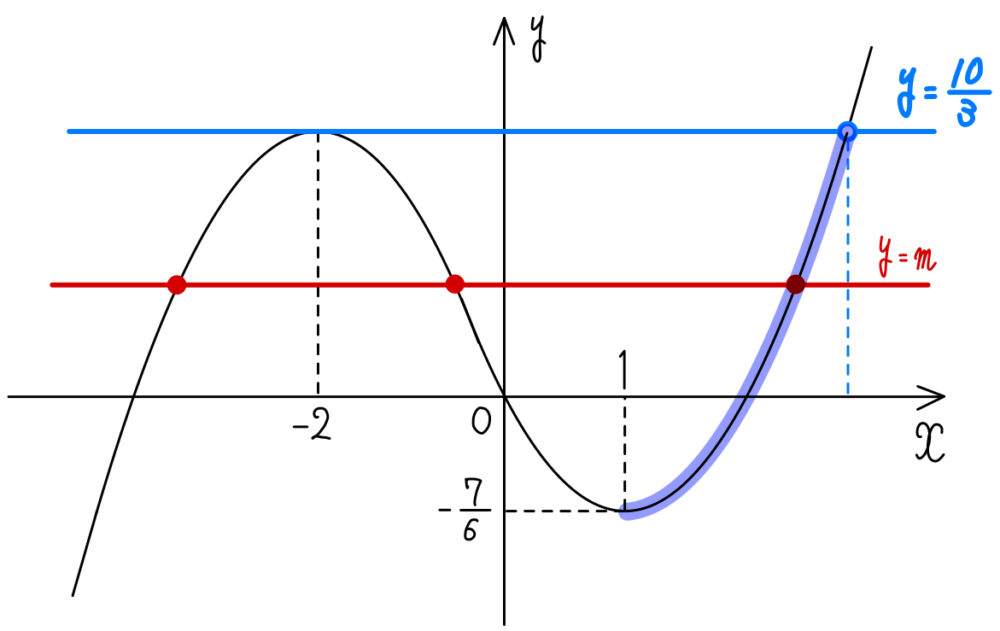
\(\gamma\) は \(y=\displaystyle\frac{1}{6}(2x^3+3x^2-12x)\) と \(y=m\) の交点の \(x\) 座標のうち最大のものであるから
\(1<\gamma<\displaystyle\frac{5}{2}\)







コメント