【2023一橋大学・第３問】
原点を \(O\) とする座標空間内に \(3\) 点 \(A(-3,2,0)\) , \(B(1,5,0)\) , \(C(4,5,1)\) がある．\(P\) は \(\left|\overrightarrow{PA}+3\overrightarrow{PB}+2\overrightarrow{PC}\right|≦36\) を満たす点である．\(4\) 点 \(O\) , \(A\) , \(B\) , \(P\) が同一平面上にないとき，四面体 \(OABP\) の体積の最大値を求めよ．
解答・解説
\(\overrightarrow{PA}+3\overrightarrow{PB}+2\overrightarrow{PC}\)
\(=\left(\overrightarrow{OA}-\overrightarrow{OP}\right)+3\left(\overrightarrow{OB}-\overrightarrow{OP}\right)+2\left(\overrightarrow{OC}-\overrightarrow{OP}\right)\)
\(=\overrightarrow{OA}+3\overrightarrow{OB}+2\overrightarrow{OC}-6\overrightarrow{OP}\) より
\(\left|\overrightarrow{PA}+3\overrightarrow{PB}+2\overrightarrow{PC}\right|≦36\)
\(\iff\) \(\left|\overrightarrow{OA}+3\overrightarrow{OB}+2\overrightarrow{OC}-6\overrightarrow{OP}\right|≦36\)
\(\iff\) \(\left|\overrightarrow{OP}-\displaystyle\frac{\overrightarrow{OA}+3\overrightarrow{OB}+2\overrightarrow{OC}}{6}\right|≦6\)
ここで \(\overrightarrow{OD}=\displaystyle\frac{\overrightarrow{OA}+3\overrightarrow{OB}+2\overrightarrow{OC}}{6}\) とおくと
点 \(P\) は中心 \(D\left(\displaystyle\frac{4}{3},\displaystyle\frac{9}{2},\displaystyle\frac{1}{3}\right)\) ，半径 \(6\) の球面および内部を動く．
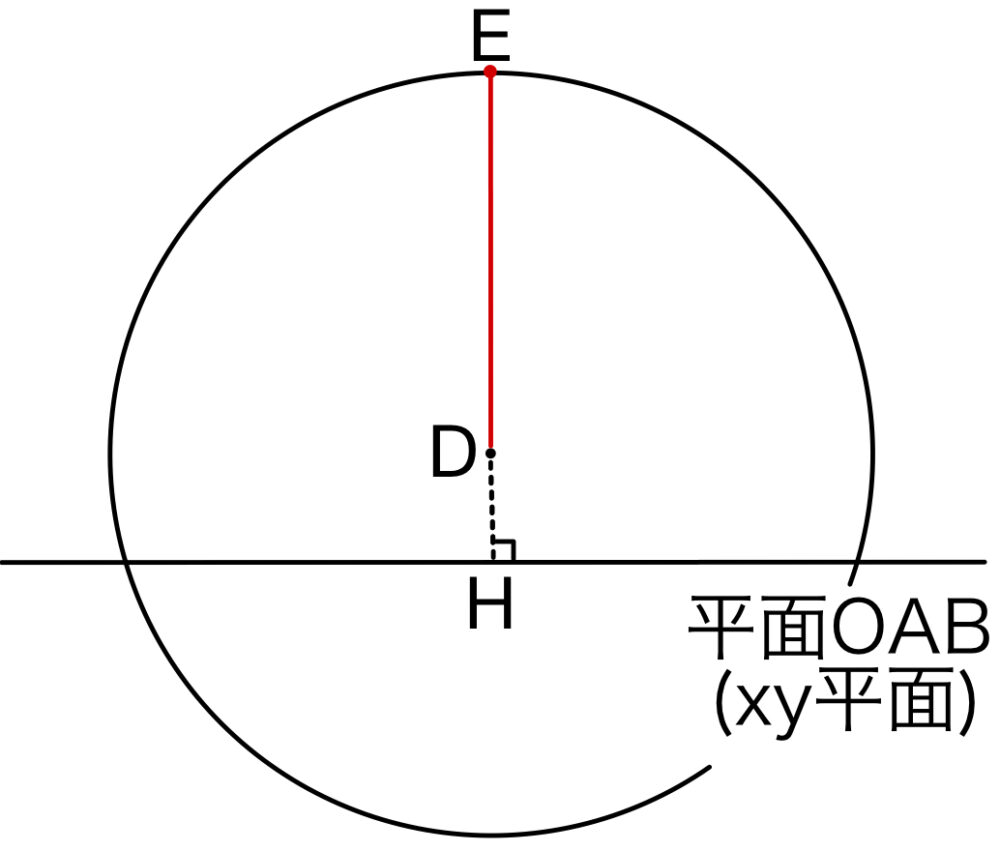点 \(D\) から平面 \(OAB\) ( \(xy\) 平面 ) に下ろした垂線の足を \(H\) とおく．
\(\triangle OAB\) を底面としたとき，四面体 \(OABP\) の体積が最大となるのは，右図のように半直線 \(HD\) と球面の交点を \(E\) としたとき
高さが \(EH\) となるときである．
\(EH=ED+DH=6+\displaystyle\frac{1}{3}=\displaystyle\frac{19}{3}\)
また \(\triangle OAB=\displaystyle\frac{1}{2}|(-3)\times 5-2\times 1|=\displaystyle\frac{17}{2}\) より
求める体積の最大値は，\(\displaystyle\frac{1}{3}\times \displaystyle\frac{17}{2}\times \displaystyle\frac{19}{3}=\displaystyle\frac{323}{18}\)
コメント