 図形と方程式
図形と方程式 2021 大阪市立大学[文系第3問]通過領域(逆像法・逆手流)
差がつく良問。受験数学では有名・頻出テーマの通過領域。数学Ⅱ。入試問題演習。
 図形と方程式
図形と方程式  三角関数
三角関数  数と式
数と式  三角関数
三角関数  式と証明
式と証明  複素数と方程式
複素数と方程式  式と証明
式と証明  式と証明
式と証明  式と証明
式と証明  式と証明
式と証明 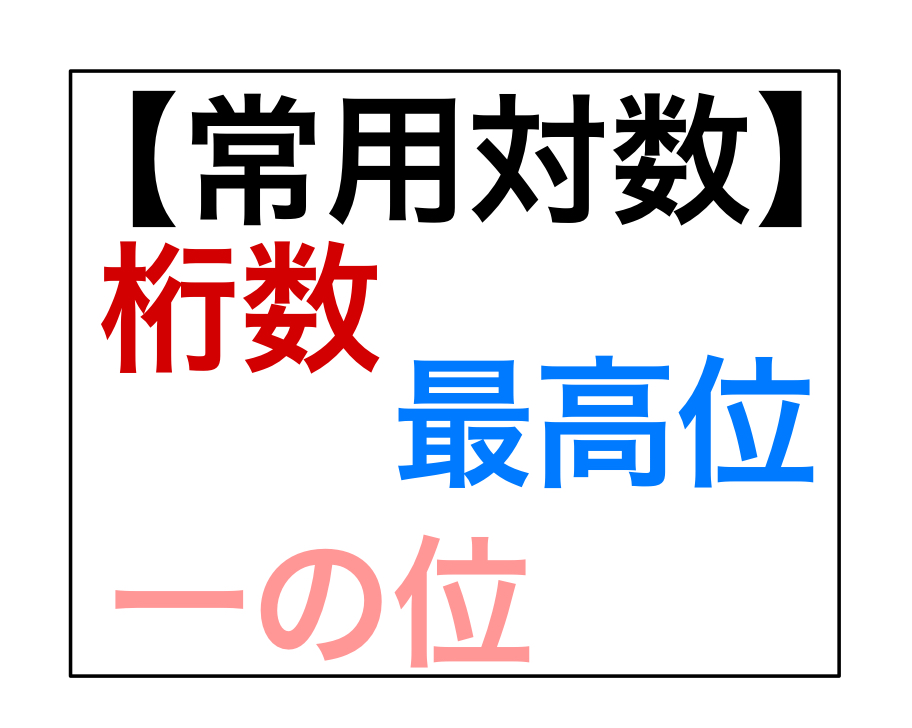 指数・対数関数
指数・対数関数  図形と方程式
図形と方程式  整数問題
整数問題  図形と方程式
図形と方程式  ベクトル
ベクトル  数学(大学入試問題)
数学(大学入試問題) 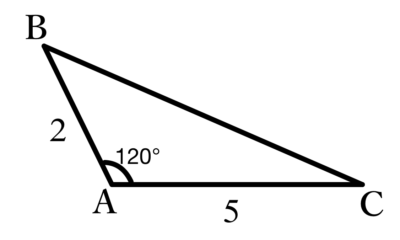 ベクトル
ベクトル