【共通接線】問題2タイプ
【問題1】
曲線 \(y=x^3+x^2+ax\) と放物線 \(y=x^2-2\) は、ともにある点 \(P\) を通り、\(P\) において共通の接線をもつ.このとき、定数 \(a\) の値を求めよ.
【問題2】
2 つの曲線 \(y=x^2\) 、\(y=-x^2+4x-4\) の共通接線の方程式を求めよ.
共通接線の解法・考え方
【タイプ⑴】共有点あり
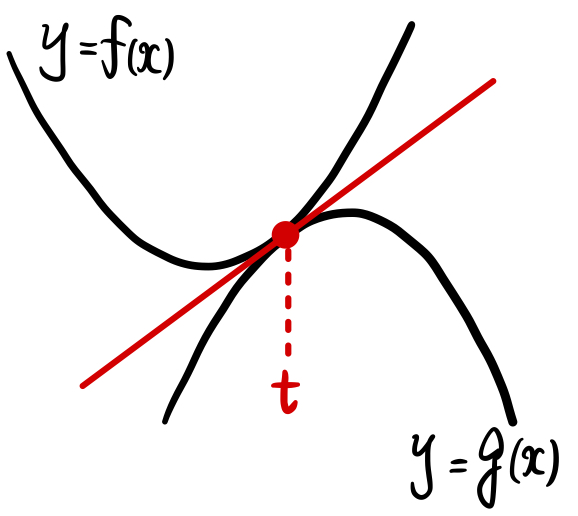
《解法の流れ》
共有点の \(x\) 座標を \(t\) とおくと
\(f(t)=g(t)\) 《 \(y\) 座標の一致》
\(f^{\prime}(t)=g^{\prime} (t)\) 《 接線の傾きの一致》
【タイプⅡ】共有点なし
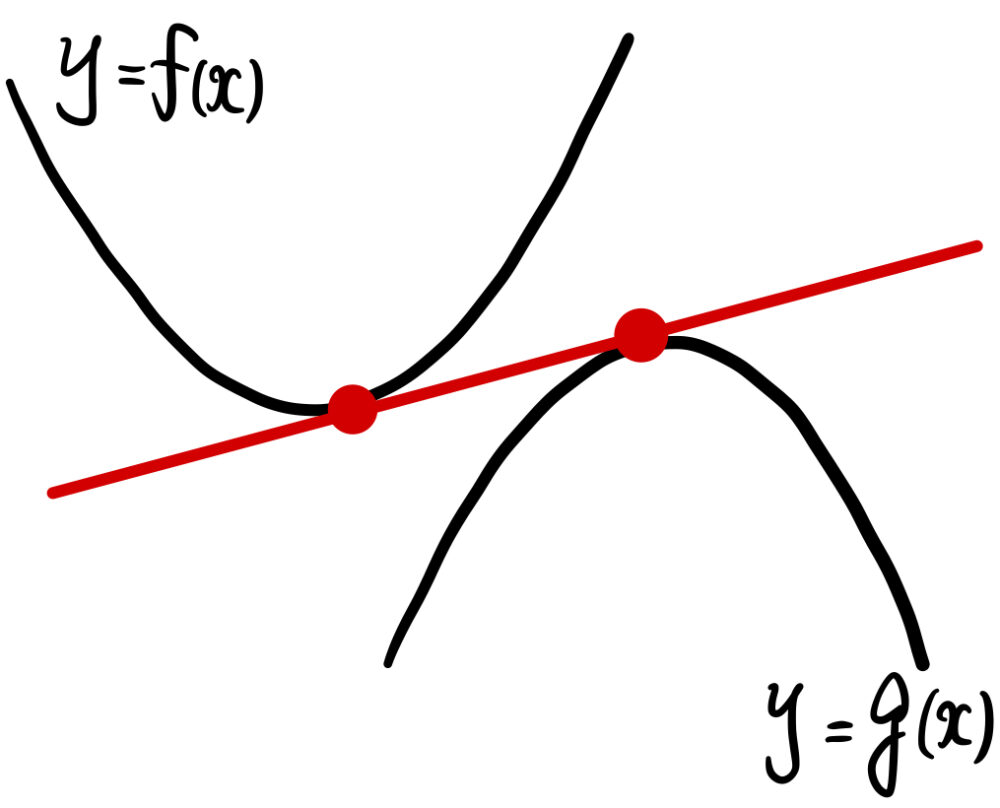
《解法の流れ》
[解法①]
一方の曲線に接点を与え、接線の方程式を求める.
その接線が、他方の曲線と接する条件を考える.
[解法②]
それぞれの曲線に接点を与え、それぞれ接線の方程式を求める.
その 2 接線が一致する条件を考える.
それぞれの解法のメリット・デメリット

問題1:解答

共有点ありの共通接線だから、タイプ⑴の問題!
\(f(x) =x^3+x^2+ax\) 、\(g(x)=x^2-2\) とおき、
点 \(P\) の \(x\) 座標を \(p\) とおく.
このとき、2 曲線は点 \(P\) において共通の接線をもつので、
\(\begin{cases}f(p)=g(p) ・・・ ①\\f^{\prime}(p)= g^{\prime}(p) ・・・② \end{cases}\)
①より
\(p^3+p^2+ap=p^2-2\)
\(p^3+ap+2=0\) ・・・ ①´
\(f^{\prime}(x) =3x^2+2x+a\) 、\(g^{\prime}(x)=2x\) で②から
\(3p^2+2p+a=2p\)
つまり、\(a=-3p^2\) ・・・ ②´
①´、②´より
\(p^3+(-3p^2)\cdot p+2=0\)
すなわち \(p^3-1=0\)
\(p\) は実数なので、\(p=1\)
②´に代入して、\(a=-3\)
問題2:解答

共有点なしの共通接線だから、タイプ⑵の問題!
2通りの解答を確認しておこう!
解法①
\(f(x)=x^2\)、\(g(x)= -x^2+4x-4\) とおく.
\(y=f(x)\) 上の接点を \(( t , t^2 )\) とおくと、
\(f^{\prime}(x)=2x\) より
接線の方程式は
\(y-t^2=2t(x-t)\)
\(y=2tx-t^2\) ・・・ ①
①と \(y=g(x)\) が接するとき
\(2tx-t^2=-x^2+4x-4\)
\(x^2+2(t-2)x-t^2+4=0\)
この式の判別式を \(D\) とすると、\(\displaystyle\frac{D}{4}=0\) となればよい
\(\displaystyle\frac{D}{4}=(t-2)^2-(-t^2+4)=0\)
\(2t^2-4t=0\)
\(2t(t-2)=0\)
\(t= 0 , 2 \)
①より
\(y=0\\y=4x-4\)
解法②
\(f(x)=x^2\)、\(g(x)= -x^2+4x-4\) とおく.
\(y=f(x)\) 上の接点を \(( t , t^2 )\) とおくと、
\(f^{\prime}(x)=2x\) より
接線の方程式は
\(y-t^2=2t(x-t)\)
\(y=2tx-t^2\) ・・・ ①
\(y=g(x)\) 上の接点を \(( s , -s^2+4s-4 )\) とおくと、
\(f^{\prime}(x)=-2x+4\) より
接線の方程式は
\(y-(-s^2+4s-4) =(-2s+4)(x-s)\)
\(y=(-2s+4)x+s^2-4\) ・・・ ②
①、②が一致するとき
\(\begin{cases}2t=-2s+4\\-t^2=s^2-4\end{cases}\)
これを解くと
\(( s , t )=( 0 , 2 ) , ( 2 , 0 )\)
①はたは②より
\(y=0\\y=4x-4\)









コメント