【2021 宮崎大学・改】
\(p\)、\(q\) を正の実数とする.点 \(O\) を原点とする座標空間において、\(4\) 点
\(A ( 1 , 1 , 0 )\)、\(B ( 0 , 2 , 0 )\)、\(C ( 0 , 0 , 6 )\)、\(D ( p , q , 1 )\)
をとる.\(3\) 点 \(A\)、\(B\)、\(C\) を含む平面を \(\alpha\) 、\(\triangle{OAD}\) の面積を \(S\) とする.
点 \(D\) が平面上 \(\alpha\) を動くとき、面積 \(S\) の最小値を求めよ.
![]()
平面の方程式について
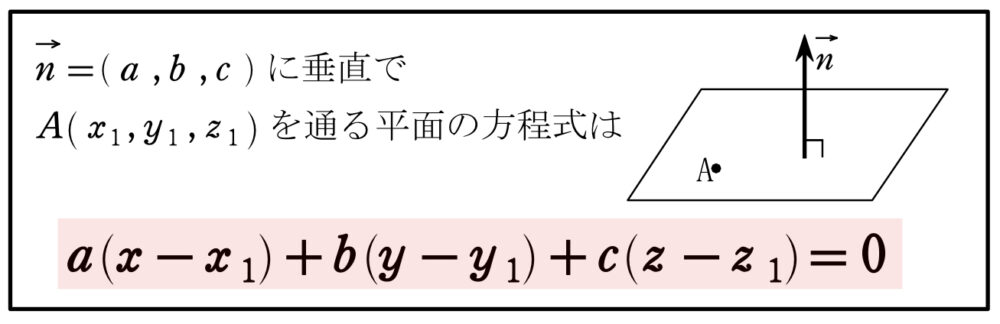
《参考》外積の利用
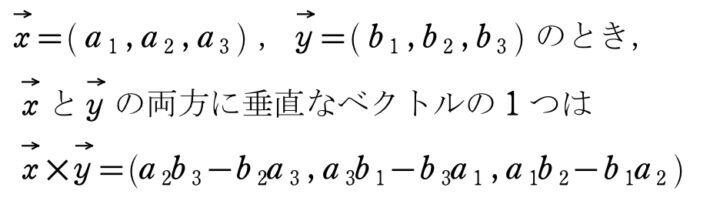
※ \(\vec{x}\times\vec{y}\) を \(\vec{x}\) と \(\vec{y}\) の外積という
※ 外積は高校数学では学習しません。(教科書に載っていません)そのため,記述式の答案で使用すると、減点される可能性があります。使用する場合は、記述として解答に残さないこと!
公式の使い方など、より詳しくは
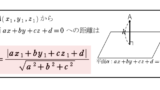
解答・考え方
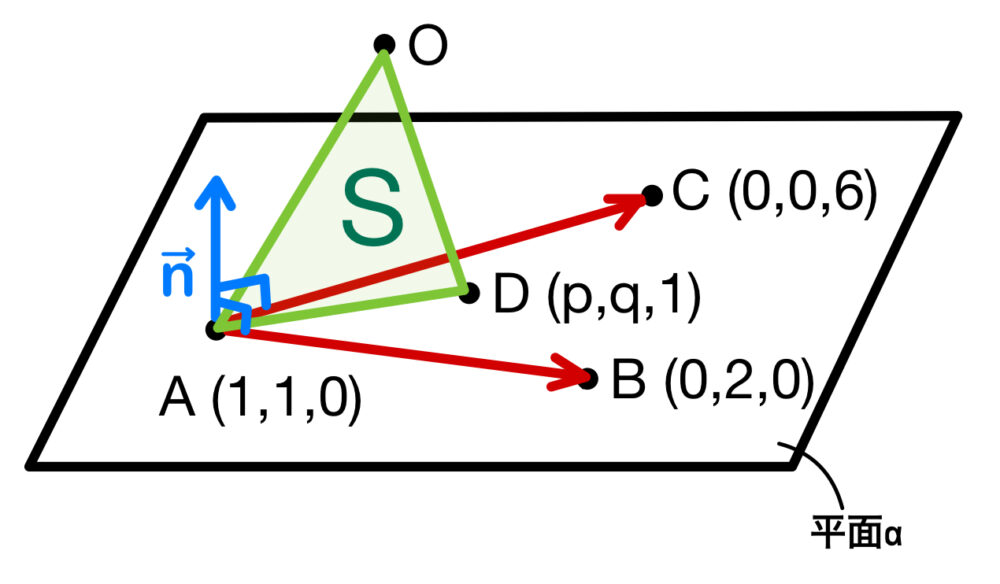
\(\overrightarrow{AB}=( -1 , 1 , 0 )\)、\(\overrightarrow{AC}=( -1 , -1 , 6 )\) の両方に垂直なベクトルを \(\vec{n}=( a , b , c )\) とおくと、
\(\overrightarrow{AB}\cdot\vec{n}=0\) かつ \(\overrightarrow{AC}\cdot\vec{n}=0\) より
\(\begin{cases}-a+b=0\\-a-b+6c=0\end{cases}\)
よって、\(a=b=3c\)
\(c=1\) として、\(\vec{n}=( 3 , 3 , 1 )\) とする.
平面 \(\alpha\) の方程式は、
\(3(x-1)+3(y-1)+z-6=0\)
\(3x+3y+z-6=0\) ・・・ ①
点 \(D\) が①上にあるとき
\(3p+3q-5=0\)
\(p+q=\displaystyle\frac{3}{5}\) ・・・ ②
また、\(S=\displaystyle\frac{1}{2}\sqrt{| \overrightarrow{OA} |^2 \times | \overrightarrow{OD} |^2-\left(\overrightarrow{OA}\cdot \overrightarrow{OD}\right)^2}\) より、
\(S=\displaystyle\frac{1}{2}\sqrt{2\times(p^2+q^2+1)-(p+q)^2}=\displaystyle\frac{1}{2}\sqrt{p^2-2pq+q^2+2} \) ・・・ ③
②で和の形が分かっている。
③は対称式
Sの最小値を求めたい
→相加平均・相乗平均の関係を利用
相加平均・相乗平均の関係の使い方については、
相加平均・相乗平均の関係はいつ使う?使うタイミングの見抜き方(基本)
相加平均・相乗平均の関係はいつ使う?使うタイミングの見抜き方(発展)
を参考にしてください。
③より、
\(S=\displaystyle\frac{1}{2}\sqrt{(p+q)^2-4pq+2}\)
②より\( S=\displaystyle\frac{1}{2}\sqrt{-4pq+\displaystyle\frac{33}{9}}\) ・・・ ④
ここで、\(p\)、\(q\) を正の実数なので、相加平均・相乗平均の関係より
\(p+q≧2\sqrt{pq}\)
②より、\(\displaystyle\frac{5}{3}≧\sqrt{pq}\)
よって\(pq≦\displaystyle\frac{25}{36}\)
④より、\(S≧\displaystyle\frac{1}{2}\sqrt{-4\times\displaystyle\frac{25}{36}+\displaystyle\frac{33}{9}}\)
したがって、\(S≧\displaystyle\frac{\sqrt{2}}{2}\)
等号成立は、
\(\begin{cases}p=q\\p+q=\displaystyle\frac{5}{3}\end{cases}\)
以上より、\(p=q=\displaystyle\frac{5}{6}\) のとき、\(S\) の最小値は\(\displaystyle\frac{\sqrt{2}}{2}\)
最後に
今回の問題は、2021宮崎大学の問題の誘導をなくし、少し条件を変えました。
もちろん様々な解法があると思いますが、ここでは難関大学で頻出テーマの「平面の方程式」を用いた解法を紹介しました。
また、入試問題における最重要テーマの1つである「相加平均・相乗平均の関係」も合わせて紹介しました。
この1問で入試問題の重要ポイントが学習できますので、ただ答えが出せるだけでなく、しっかりと考え方を大切にしてください!








コメント