【2022数学ⅠA】第１問[３](図形と計量)
問題と解答・解説《ソ〜ヒ》
解答・解説《ソ〜ヒ》
(１)
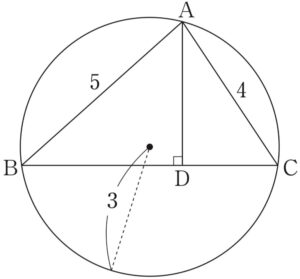正弦定理より( \(R\) は外接円の半径 )
\(2R=\displaystyle\frac{AC}{\sin \angle ABC}\) \(\iff\) \(2\times 3=\displaystyle\frac{4}{\sin \angle ABC}\)
よって \(\sin \angle ABC=\displaystyle\frac{2}{3}\) ・・・《ソタ》
次に \(\triangle ABD\) に注目して三角比の定義より
\(\sin \angle ABC=\displaystyle\frac{AD}{AB}\) \(\iff\) \(\displaystyle\frac{2}{3}=\displaystyle\frac{AD}{5}\)
よって \(AD=\displaystyle\frac{10}{3}\) ・・・《チツテ》
(２)
\(AB=x\) , \(AC=y\) とおくと
\(2x+y=14\) \(\iff\) \(y=-2x+14\) ・・・②
円の弦の長さは円の直径以下なので
\(0<x≦6\) かつ \(0<y≦6\)
①より
\(0<x≦6\) かつ \(0<-2x+14≦6\)
よって \(4≦x≦6\)
\(4≦AB≦6\) ・・・《トナ》
また，(１)と同様に
正弦定理より \(2\times 3=\displaystyle\frac{y}{\sin \angle ABC}\)
\(\iff\) \(\sin \angle ABC=\displaystyle\frac{y}{6}\)
①より
\(\sin \angle ABC=\displaystyle\frac{-2x+14}{6}=\displaystyle\frac{-x+7}{3}\) であり，
三角比の定義から \(\sin \angle ABC=\displaystyle\frac{AD}{x}\) であるので
\(AD=x\cdot\sin \angle ABC=x\cdot\displaystyle\frac{-x+7}{3}=\displaystyle\frac{-1}{3}x^2+\displaystyle\frac{7}{3}x\)
よって，\(AD=\)\(\displaystyle\frac{-1}{3}AB^2+\displaystyle\frac{7}{3}AB\) ・・・《ニ〜ハ》
\(AD=\)\(\displaystyle\frac{-1}{3}x^2+\displaystyle\frac{7}{3}x=-\displaystyle\frac{1}{3}\left(x-\displaystyle\frac{7}{2}\right)^2+\displaystyle\frac{49}{12}\)
\(4≦x≦6\) であることに注意すると
\(x=4\) のとき \(AD\) は最大値 \(4\) ・・・《ヒ》
コメント