【2021数学ⅠA(第2日程)】第２問[２](データの分析)
(１)問題と解答・解説《ツ》
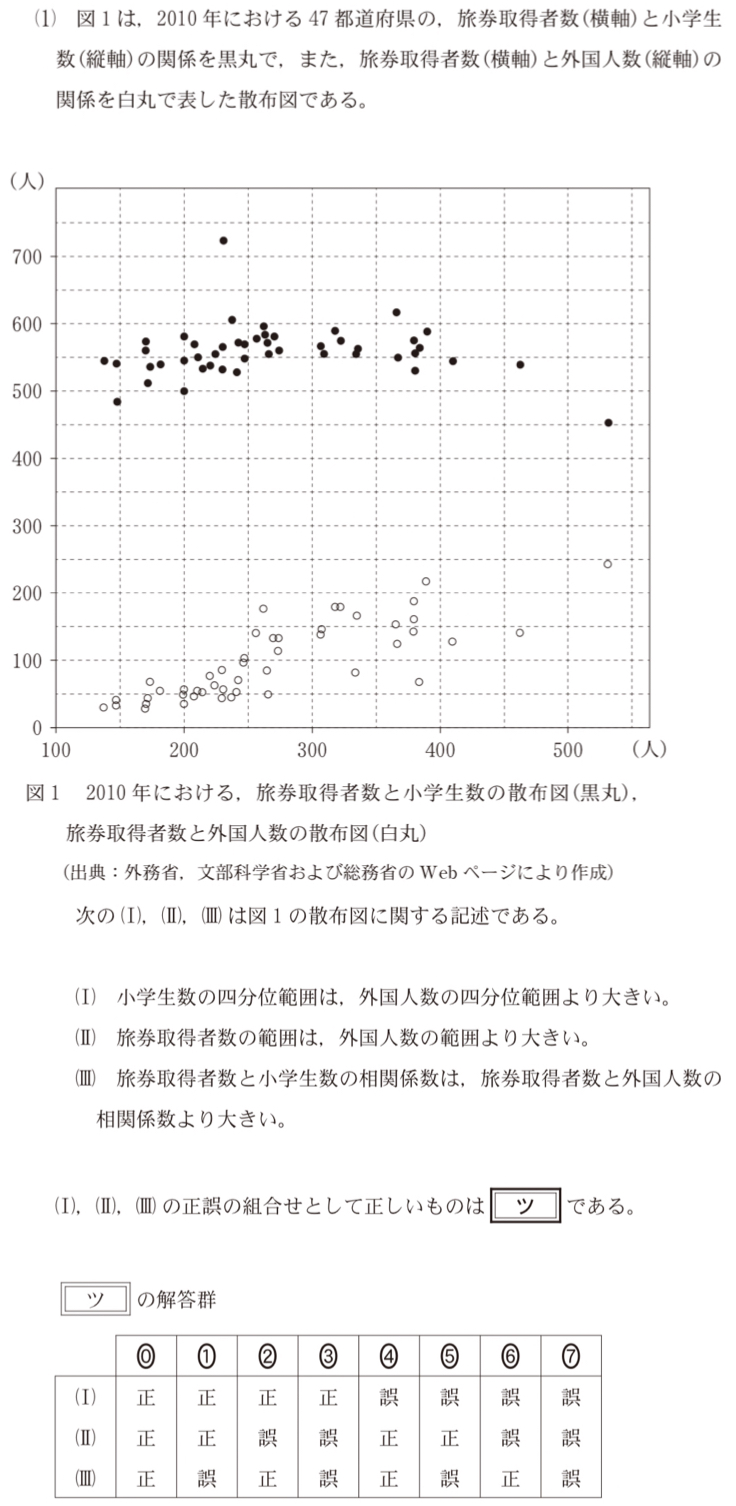
(１)解答・解説《ツ》
( Ⅰ ) 誤
「四分位範囲」は，第 \(3\) 四分位数から第 \(1\) 四分位数を引いたものですね！
また，本文はデータの大きさが \(47\) ですから，第 \(1\) 四分位数は小さい方から \(12\) 番目，第 \(3\) 四分位数は小さい方から \(36\) 番目ですね！
小学生数については，第 \(1\) 四分位数が約 \(540\) 人，第 \(3\) 四分位数が約 \(570\) 人であるから，
四分位範囲は，\(570-540=30\) 人
外国人数については，第 \(1\) 四分位数が約 \(50\) 人，第 \(3\) 四分位数が約 \(140\) 人であるから，
四分位範囲は，\(140-50=90\) 人
したがって，外国人数の四分位範囲の方が大きいため「誤」です
( Ⅱ ) 正
「範囲」は最大値から最小値を引いたものです！
旅券取得者数については，最大値が約 \(530\) 人，最小値が約 \(130\) 人であるから，
範囲は \(530-130=400\) 人
外国人数については，最大値が約 \(250\) 人，最小値が約 \(25\) 人であるから，
範囲は \(250-25=225\) 人
したがって「正」である．
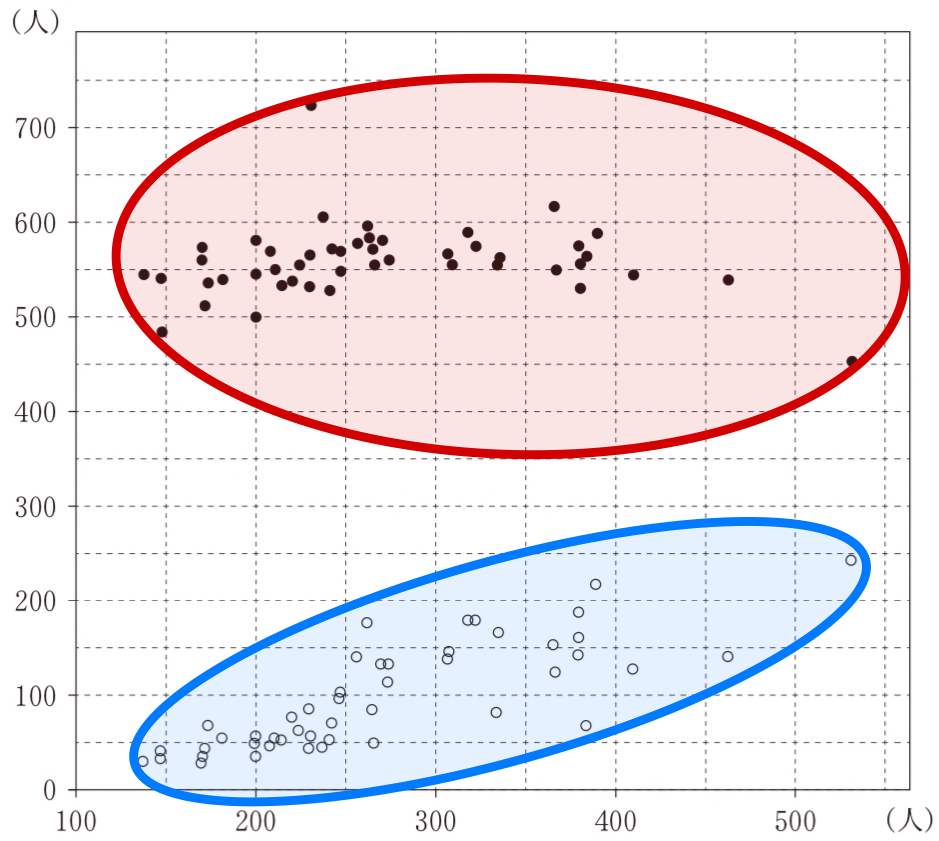( Ⅲ ) 誤
旅券取得者数と小学生数の相関関係はほとんどない．
一方で，旅券取得者数と外国人数には正の相関が見られる．
以上から，「誤，正，誤」であるため，《ツ：⑤》
(２)問題と解答・解説《テ〜二》
(２)解答・解説《テ〜二》
条件から，
\(\overline{x}=\displaystyle\frac{1}{n}\left\{x_{1}f_{1}+x_{2}f_{2}+x_{3}f_{3}+\cdots+x_{k}f_{k}\right\}\)
\(=\displaystyle\frac{1}{n}\left[x_{1}f_{1}+(x_{1}+h)f_{2}+(x_{1}+2h)f_{3}+\cdots+\left\{x_{1}+(k-1)h\right\}f_{k}\right]\)
\(=\displaystyle\frac{1}{n}\left[x_{1}(f_{1}+f_{2}+f_{3}+\cdots+f_{k})+h\left\{f_{2}+2f_{3}+\cdots+(k-1)f_{k}\right\}\right]\)
ここで，\(f_{1}+f_{2}+f_{3}+\cdots+f_{k}=n\) であるから，
\(\overline{x}=\displaystyle\frac{1}{n}\left[nx_{1}+h\left\{f_{2}+2f_{3}+\cdots+(k-1)f_{k}\right\}\right]\)
\(=x_{1}+\displaystyle\frac{h}{n}\left\{f_{2}+2f_{3}+\cdots+(k-1)f_{k}\right\}\)
したがって，《テ：③》
次に，\(2008\) 年における旅券取得者数のヒストグラムから
| 階級値 | \(100\) | \(200\) | \(300\) | \(400\) | \(500\) | 計 |
| 度 数 | \(4\) | \(25\) | \(14\) | \(3\) | \(1\) | \(47\) |
であるので，\(x_{1}=100\) ，\(h=100\) ，\(n=47\) とすると
\(\overline{x}=100+\displaystyle\frac{100}{47}(25+2\times 14+3\times 3+4\times 1)=240.42\cdots\)
小数第 \(1\) 位を四捨五入すると，\(240\) ・・・《ト〜ニ》
(３)問題と解答・解説《ヌ〜ハ》
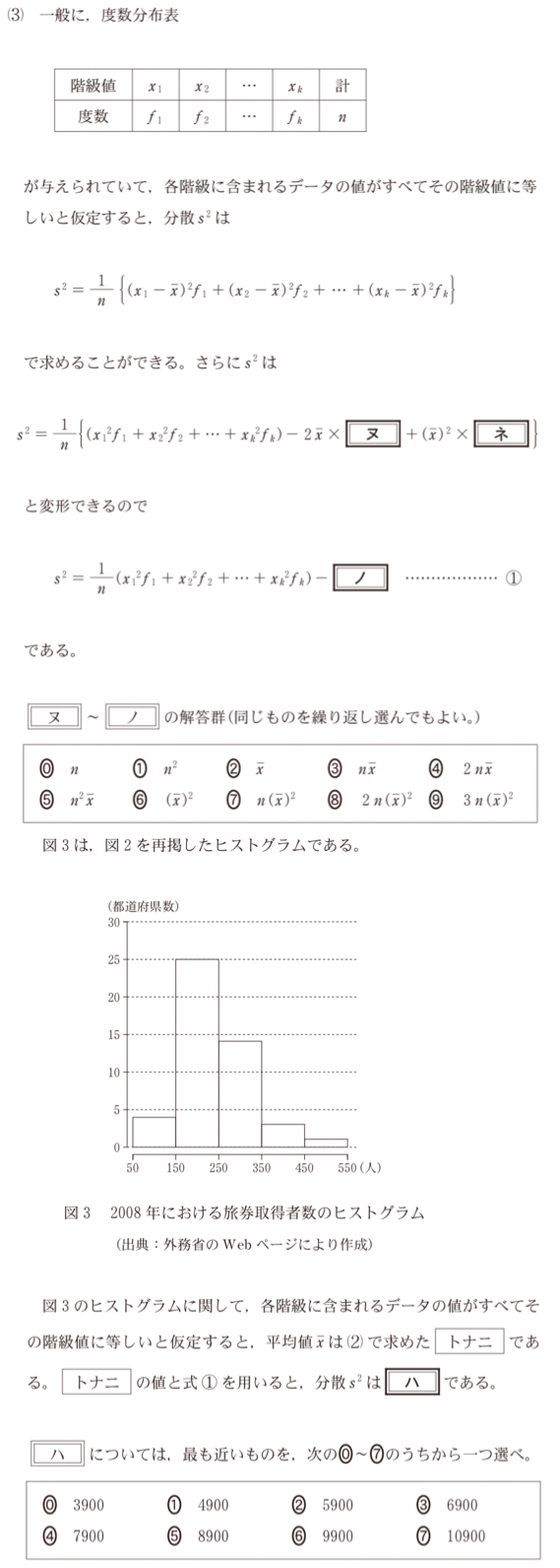
(３)解答・解説《ヌ〜ハ》
\(s^2=\displaystyle\frac{1}{n}\left\{\left(x_{1}-\overline{x}\right)^2f_{1}+\left(x_{2}-\overline{x}\right)^2f_{2}+\cdots+\left(x_{k}-\overline{x}\right)^2f_{k}\right\}\)
\(=\displaystyle\frac{1}{n}\left\{(x_{1}^2f_{1}+x_{2}^2f_{2}+\cdots+x_{k}^2f_{k})\\-2\overline{x}(x_{1}f_{1}+x_{2}f_{2}+\cdots+x_{k}f_{k})+\left(\overline{x}\right)^2(f_{1}+f_{2}+\cdots+f_{k})\right\}\)
\(=\displaystyle\frac{1}{n}\left\{(x_{1}^2f_{1}+x_{2}^2f_{2}+\cdots+x_{k}^2f_{k})-2\overline{x}\times n\overline{x}+\left(\overline{x}\right)^2\times n\right\}\)
と変形できるので，
\(s^2=\displaystyle\frac{1}{n}(x_{1}^2f_{1}+x_{2}^2f_{2}+\cdots+x_{k}^2f_{k})-\left(\overline{x}\right)^2\)
したがって，《ヌ：③，ネ：⓪，ノ：⑥》
(２) より，\(\overline{x}=240\) として
\(s^2=\displaystyle\frac{1}{47}(100^2\times 4+200^2\times 25+300^2\times 14+400^2\times 3+500^2\times 1)-240^2\)
これを計算すると，\(s^2=6868.08\cdots\)
選択肢の中から最も近い値は，③6900 ・・・《ハ》
コメント