\(n\) を \(3\) 以上の整数とする.\(1\) 個のさいころを \(n\) 回投げたときに、出た目を大きい順に並べたものを \(X_{1} , X_{2} , \cdots , X_{n}\) ( \(X_{1}≧X_{2}≧\cdots≧X_{n}\) ) とする.
例えば、\(1\) 個のさいころ \(5\) 回投げて、出た目が順に \(4 , 5 , 3 , 4 , 2\) であったとすると、
\(X_{1}=5 , X_{2}=4 , X_{3}=4 , X_{4}=3 , X_{5}=2\) となる.
\(1\) 個のさいころを \(n\) 回投げたとき、次の事象が起る確率をそれぞれ求めよ.
(1) \(X_{n}=2\)
(2) \(X_{2}=6\)
(3) \(X_{2}=6\) かつ \(X_{n}=2\)
考え方
『最小値が \(k\) の確率』
=『最小値が \(k\) 以上の確率』ー『最小値が \(k+1\) 以上の確率』
頻出問題の1つです!様々な大学で出題されていますので、この考え方はしっかりと身につけておきましょう!
解答
(1) \(X_{n}=2\) となるのは、最小のさいころの目が \(2\) である.
よって、\(n\) 個のさいころにおいて、
「すべてが \(2\) 以上」 から、「すべてが \(3\) 以上」となる場合を除けばよい.
したがって求める確率は、\(\left(\displaystyle\frac{5}{6}\right)^n-\left(\displaystyle\frac{4}{6}\right)^n=\displaystyle\frac{5^n-4^n}{6^n}\)
(2) \(X_{2}=6\) となるのは、「少なくとも \(2\) 回は \(6\) の目が出る」ことである.
その余事象は、「\(6\) の目が \(0\) 回」または「\(6\) の目が \(1\) 回」
(ア) \(6\) の目が \(0\) 回のとき
\(n\) 個すべてのさいころが \(1\) ~ \(5\) の目が出ればよいので、\(\left(\displaystyle\frac{5}{6}\right)^n\)
(イ) \(6\) の目が \(1\) 回のとき
\(n\) 回のうち、何回目で \(6\) の目が出るか \(n\) 通りあるので、
\(n\cdot\left(\displaystyle\frac{1}{6}\right)\cdot\left(\displaystyle\frac{5}{6}\right)^{n-1}\)
したがって求める確率は、
\(1-\left(\displaystyle\frac{5}{6}\right)^n-n\cdot\left(\displaystyle\frac{1}{6}\right)\cdot\left(\displaystyle\frac{5}{6}\right)^{n-1}=\displaystyle\frac{6^n-5^n-n\cdot5^{n-1}}{6^n}\)
(3) 事象 \(A\)、\(B\)、\(C\)、\(D\)を
\(A\):すべてが \(2\) 以上
\(B\):すべてが \(3\) 以上
\(C\):\(6\) の目が \(0\) 回
\(D\):\(6\) の目が \(1\) 回
とすると、\(A\)、\(B\)、\(C\)、\(D\)は下図のベン図のような関係で表され、
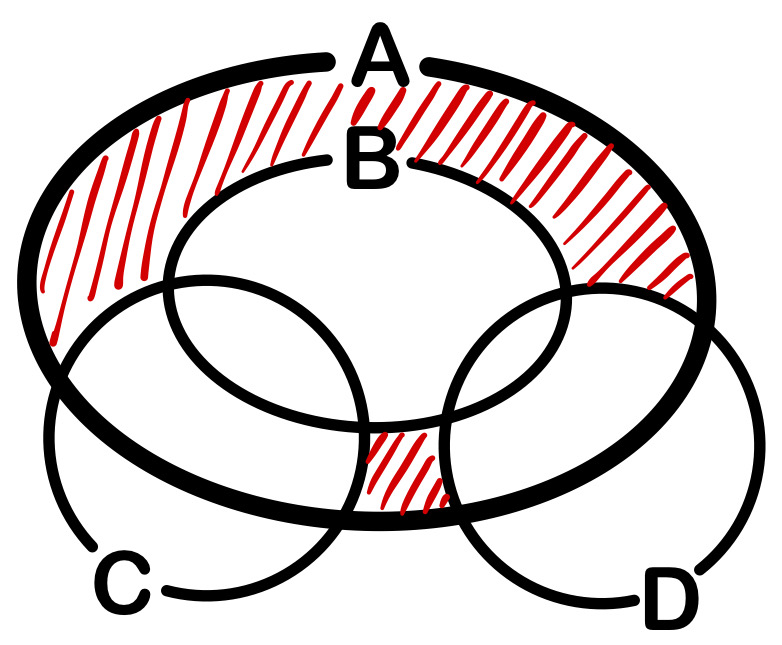
\(X_{2}=6\) かつ \(X_{n}=2\) はベン図の斜線部である.
この事象が起る確率は、
\(P(A)-P(B)-P(A\cap C)-P(A\cap D)+P(B\cap C)+P(B\cap D)\) ・・・①
\(P(B\cap C)\) は「すべてが \(3 , 4 , 5\) 」となる確率であるから、
\(P(B\cap C)=\displaystyle\frac{3^n}{6^n}\)
また、\(P(B\cap D)\) は「\(6\) が \(1\) 回、他は \( 3 , 4 , 5\)」となる確率であるから、
\(P(B\cap D)=\displaystyle\frac{n\cdot3^{n-1}}{6^n}\)
同様に考え、
\(P(A\cap C)=\displaystyle\frac{4^n}{6^n}\)
\(P(A\cap D)=\displaystyle\frac{n\cdot4^{n-1}}{6^n}\)
①より、求める確率は、
\(\displaystyle\frac{5^n-2\cdot4^n-n\cdot4^{n-1}+3^n+n\cdot3^{n-1}}{6^n}\)








コメント