直方体 \(ABCD-EFGH\) において、次の条件が与えられたときの直方体の体積の最大値 \(V\) を考える.
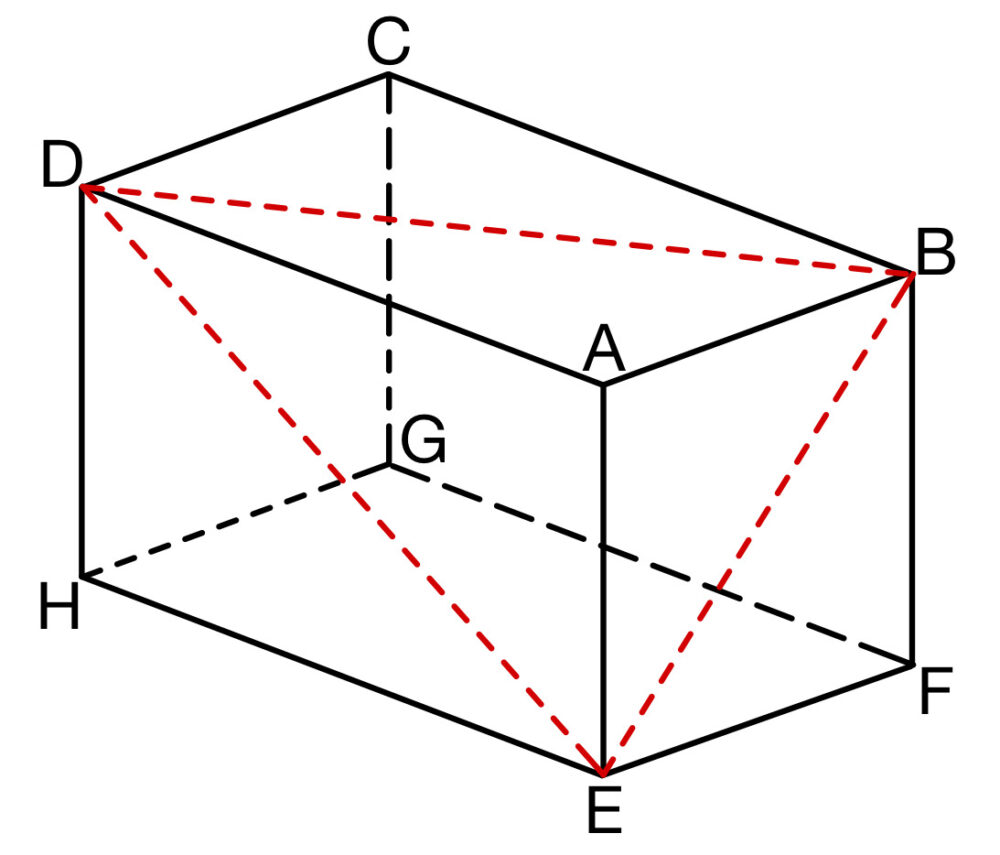
(1) \(AB+2AD+3AE=1\) のとき、\(V\) を求めよ.
(2) \(AB+AD+AE+BD+DE+BE=1\) のとき、\(V\) を求めよ.
考え方
\(AB=a\)、\(AD=b\)、\(AE=c\) とすると、
直方体の体積は \(abc\) (☜積の形)
また条件から、\(a+2b+3c=1\) (☜和の形)
\(3\) つの相加平均・相乗平均の関係
\(a≧0\)、\(b≧0\)、\(c≧0\) のとき
\(\displaystyle\frac{a+b+c}{3}≧\sqrt[3]{abc}\)
等号成立は \(a=b=c\) のとき
相加相乗を使うタイミングなどについては、以下の記事を参考にしてください!
相加平均・相乗平均の関係はいつ使う?使うタイミングの見抜き方(基本)
相加平均・相乗平均の関係はいつ使う?使うタイミングの見抜き方(発展)
相加平均・相乗平均の関係については、ただ公式を覚えているだけでは役に立ちません。
入試問題でも頻出テーマの1つですから、しっかりと使いこなせることが出来るように!![]()
解答
\(AB=a\)、\(AD=b\)、\(AE=c\) とする.
このとき直方体の体積は \(abc\)
また条件から、\(a+2b+3c=1\) ・・・①
相加平均・相乗平均の関係より
\(a+2b+3c≧3\sqrt[3]{a\cdot 2b\cdot 3c}=3\sqrt[3]{6abc}\)
①より
\(1≧3\sqrt[3]{6abc}\)
\(abc≦\displaystyle\frac{1}{162}\)
等号成立は、\(a=2b=3c\) かつ \(a+2b+3c=1\)
つまり、\(a=\displaystyle\frac{1}{3}\)、\(b=\displaystyle\frac{1}{6}\)、\(c=\displaystyle\frac{1}{9}\) のとき、\(V=\displaystyle\frac{1}{162}\)
(2) 相加平均・相乗平均の関係より
\(a^2+b^2≧2\sqrt{a^2b^2}=2ab\)
同様に、\(b^2+c^2≧2bc\)、\(c^2+a^2≧2ca\)
また、\(AB+AD+AE+BD+DE+BE=1\) より
\(a+b+c+\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}=1\) ・・・②
\(a+b+c+\sqrt{a^2+b^2}+\sqrt{b^2+c^2}+\sqrt{c^2+a^2}\\≧a+b+c+\sqrt{2}(\sqrt{ab}+\sqrt{bc}+\sqrt{ca})\\3\sqrt[3]{a\cdot b\cdot c}+\sqrt{2}\cdot 3\sqrt[3]{ \sqrt{ab}\cdot \sqrt{bc}\cdot \sqrt{ca}}\\≧3\sqrt[3]{a\cdot b\cdot c}+3\sqrt{2}\sqrt[3]{abc}\\=3(\sqrt{2}+1) \sqrt[3]{abc}\)
②より
\(1≧3(\sqrt{2}+1) \sqrt[3]{abc}\)
よって、\(abc≦\displaystyle\frac{1}{3(\sqrt{2}+1)}= \displaystyle\frac{-7+5\sqrt{2}}{27}\)
等号成立は、\(a=b=c=\displaystyle\frac{\sqrt{2}-1}{3}\) のとき
\(V=\displaystyle\frac{-7+5\sqrt{2}}{27}\)










コメント