【2004京都大学(文)】角の二等分線と円のベクトル方程式の交点の位置ベクトル

【2004京都大学(文)】

\(\triangle OAB\) において，\(\overrightarrow{a}=\overrightarrow{OA}\) ,\(\overrightarrow{b}=\overrightarrow{OB}\) とする．

\(\left|\overrightarrow{a}\right|=3\) , \(\left|\overrightarrow{b}\right|=5\) , \(\cos\angle AOB=\displaystyle\frac{3}{5}\)

とする．このとき，\(\angle AOB\) の \(2\) 等分線と，\(B\) を中心とする半径 \(\sqrt{10}\) の円との交点の，\(O\) を原点とする位置ベクトルを \(\overrightarrow{a}\) , \(\overrightarrow{b}\) を用いてあらわせ．

角の二等分線のベクトル
円のベクトル方程式
解答

角の二等分線のベクトル

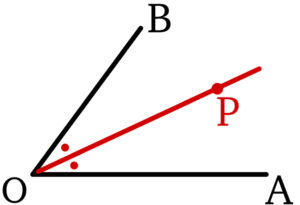一直線上にない \(3\) 点 \(O\) , \(A\) , \(B\) に対して，\(\angle AOB\) の二等分線上の点を \(P\) とするとき，実数 \(t\) を用いて

\(\overrightarrow{OP}=t\left(\displaystyle\frac{\overrightarrow{OA}}{\left|\overrightarrow{OA}\right|}+\displaystyle\frac{\overrightarrow{OB}}{\left|\overrightarrow{OB}\right|}\right)\)

※ とても有名な形です。結果を覚えておきましょう！証明等については⏬

【2006神戸大学・文】角の二等分線のベクトル｜差がつく良問

数学B平面ベクトル。内角の二等分線のベクトルの公式・証明・利用。差がつく有名問題。４STEP発展問題にものっている問題。２次試験数学対策。

円のベクトル方程式

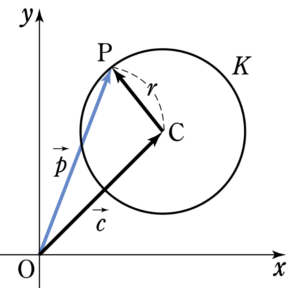点 \(C\) ( \(\overrightarrow{c}\) ) を中心とする半径 \(r\) の円を \(K\) とする．

このとき，点 \(P\) ( \(\overrightarrow{p}\) ) が円 \(K\) 上にあることは，

\(|\overrightarrow{p}-\overrightarrow{c}|=r\)

と表すことができる．これを円のベクトル方程式という．

解答

交点を \(P\) とする．点 \(P\) は \(\angle AOB\) の二等分線上より実数 \(t\) を用いて，

\(\overrightarrow{OP}=t\left(\displaystyle\frac{\overrightarrow{OA}}{\left|\overrightarrow{OA}\right|}+\displaystyle\frac{\overrightarrow{OB}}{\left|\overrightarrow{OB}\right|}\right)=t\left(\displaystyle\frac{\overrightarrow{a}}{3}+\displaystyle\frac{\overrightarrow{b}}{5}\right)\) ・・・①

とおける．

また，点 \(P\) は \(B\) を中心として半径 \(\sqrt{10}\) の円上より

\(|\overrightarrow{p}-\overrightarrow{b}|=\sqrt{10}\)

①より

\(\left|\displaystyle\frac{t}{3}\overrightarrow{a}+\left(\displaystyle\frac{t}{5}-1\right)\overrightarrow{b}\right|=\sqrt{10}\)

\(2\) 乗すると

\(\displaystyle\frac{t^2}{9}\left|\overrightarrow{a}\right|^2+\displaystyle\frac{2t}{3}\left(\displaystyle\frac{t}{5}-1\right)\overrightarrow{a}\cdot\overrightarrow{b}+\left(\displaystyle\frac{t}{5}-1\right)^2\left|\overrightarrow{b}\right|^2=10\)

ここで，\(\left|\overrightarrow{a}\right|^2=3^2=9\) , \(\left|\overrightarrow{b}\right|^2=5^2=25\)

\(\overrightarrow{a}\cdot\overrightarrow{b}=3\times 5\times \displaystyle\frac{3}{5}=9\) より

代入して式を整理すると，

\(16t^2-80t+75=0\)

\((4t-5)(4t-15)=0\)

よって，\(t=\displaystyle\frac{5}{4} , \displaystyle\frac{15}{4}\)

したがって①より

\(\overrightarrow{OP}=\displaystyle\frac{5}{12}\overrightarrow{a}+\displaystyle\frac{1}{4}\overrightarrow{b}\)

\(\overrightarrow{OP}=\displaystyle\frac{5}{4}\overrightarrow{a}+\displaystyle\frac{3}{4}\overrightarrow{b}\)