【2013京都大学(文理共通)】
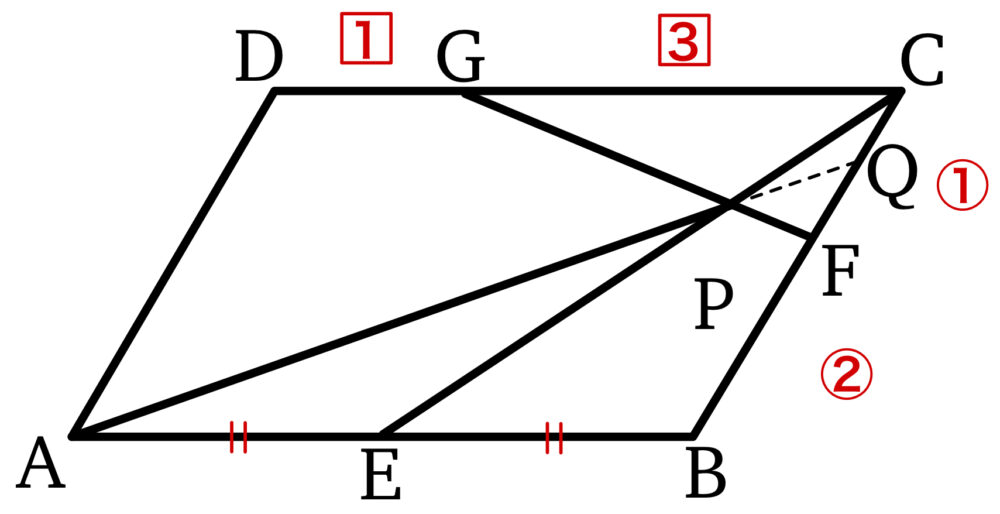
平行四辺形 \(ABCD\) において，辺 \(AB\) を \(1 : 1\) に内分する点を \(E\)，辺 \(BC\) を \(2 : 1\) に内分する点を \(F\)，辺 \(CD\) を \(3 : 1\) に内分する点を \(G\) とする．線分 \(CE\) と線分 \(FG\) の交点を \(P\) とし，線分 \(AP\) を延長した直線と辺 \(BC\) の交点を \(Q\) とするとき，比 \(AP : PQ\) を求めよ．
平面図形の問題は３つのアプローチ！
平面図形の問題
👉 ３つのアプローチ！
① 幾何(三角比・合同・相似など)
② 座標
③ ベクトル
(数学Ⅲを履修している人は④複素数平面，⑤極座標など)
えっ？？ベクトルの問題だからベクトルで解くのでは・・・？
もちろんベクトルで解くのが一般的です。
ただ勝手に分野を決めつけることはNG！
平面図形は差がつく分野になりますから，常に３つのアプローチを考える癖をつけておきましょう！
なぜ３つのアプローチを考えるかについては「【差がつく考え方】平面図形の３つのアプローチ！(幾何・座標・ベクトル)」を確認しましょう！
方針①ベクトルの利用
共線条件
共線条件とは，異なる \(3\) 点が一直線上に並ぶときの条件
\(3\) 点 \(A\)，\(B\)，\(P\) が一直線上にあるとき
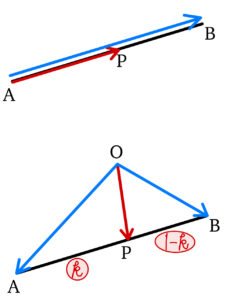① \(A\) を始点として考える( \(k\) は実数 )
\(\overrightarrow{AP}=k\overrightarrow{AB}\)
② 内分の公式の利用
\(AP : PB = k : 1-k\) とするとき
\(\overrightarrow{OP}=(1-k)\overrightarrow{OA}+k\overrightarrow{OB}\)
③ ベクトル方程式
\(\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}\) かつ \(s+t=1\)
( ただし， \(s\)， \(t\) は実数 )
※ ①〜③は本質的にはすべて同じこと！
・②は①の始点を \(A\) から \(O\) に変換しただけである．
・③は②において，\(s=1-k\) , \(t=k\) とおいた．
一次独立(平面のベクトル)
\(\overrightarrow{a}≠\overrightarrow{0}\) , \(\overrightarrow{b}≠\overrightarrow{0}\) , \(\overrightarrow{a}\) と \(\overrightarrow{b}\) が平行でないとき
\(m_{1}\overrightarrow{a}+n_{1}\overrightarrow{b}=m_{2}\overrightarrow{a}+n_{2}\overrightarrow{b}\)
\(\iff\) \(m_{1}=m_{2}\) , \(n_{1}=n_{2}\)
ベクトルで係数比較したいときは必ず一次独立なベクトルであることを記述しましょう！
方針の立て方
平面図形であるから，まず基準にする \(2\) つのベクトルを設定する！
\(\overrightarrow{AB}=\overrightarrow{x}\) , \(\overrightarrow{AD}=\overrightarrow{y}\) とおく．
点 \(P\) は『 線分 \(CE\) 上 』かつ『 線分 \(FG\) 上 』であるから，
それぞれから共線条件を利用して\(\overrightarrow{AP}\) を表現する．
しかしそれらはそれぞれ等しいベクトルであるから，一次独立の性質から係数比較をして処理する！
解答
\(\overrightarrow{AB}=\overrightarrow{x}\) , \(\overrightarrow{AD}=\overrightarrow{y}\) とおく．
点 \(P\) は線分 \(CE\) 上より
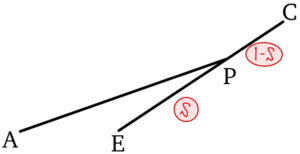
実数 \(s\) ( \(0 ≦ s ≦ 1 \) ) を用いて
\(EP : PC = s : 1-s\) とおくと
\(\overrightarrow{AP}=(1-s)\overrightarrow{AE}+s\overrightarrow{AC}\)
ここで，\(\overrightarrow{AE}=\displaystyle\frac{1}{2}\overrightarrow{x}\) , \(\overrightarrow{AC}=\overrightarrow{x}+\overrightarrow{y}\) より
\(\overrightarrow{AP}=(1-s)\cdot \displaystyle\frac{1}{2}\overrightarrow{x}+s(\overrightarrow{x}+\overrightarrow{y})\)
よって，\(\overrightarrow{AP}=\displaystyle\frac{s+1}{2}\overrightarrow{x}+s\overrightarrow{y}\) ・・・①
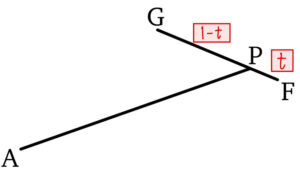点 \(P\) は線分 \(FG\) 上より
実数 \(t\) ( \(0 ≦ t ≦ 1 \) ) を用いて
\(FP : PG = t : 1-t\) とおくと
\(\overrightarrow{AP}=(1-t)\overrightarrow{AF}+t\overrightarrow{AG}\)
ここで，\(\overrightarrow{AF}=\overrightarrow{x}+\displaystyle\frac{2}{3}\overrightarrow{y}\) , \(\overrightarrow{AG}=\displaystyle\frac{1}{4}\overrightarrow{x}+\overrightarrow{y}\) より
\(\overrightarrow{AP}=(1-t)\left(\overrightarrow{x}+\displaystyle\frac{2}{3}\overrightarrow{y}\right)+t\left(\displaystyle\frac{1}{4}\overrightarrow{x}+\overrightarrow{y}\right)\)
よって，\(\overrightarrow{AP}=\displaystyle\frac{-3t+4}{4}\overrightarrow{x}+\displaystyle\frac{t+2}{3}\overrightarrow{y}\) ・・・②
\(\overrightarrow{x}≠\overrightarrow{0}\) , \(\overrightarrow{y}≠\overrightarrow{0}\) , \(\overrightarrow{x}\) と \(\overrightarrow{y}\) が平行でない(\(\overrightarrow{x}\) , \(\overrightarrow{y}\) は一次独立)であるから，①，②より
記述において①，②の係数比較を行う際に，必ず一次独立であることの記述を行いましょう！記述がない場合，大幅な減点になります！
\(\begin{cases}\displaystyle\frac{s+1}{2}=\displaystyle\frac{-3t+4}{4}\\s=\displaystyle\frac{t+2}{3} \end{cases}\) \(\iff\) \(\begin{cases}s=\displaystyle\frac{8}{11}\\t=\displaystyle\frac{2}{11} \end{cases}\)
①(または②)より，\(\overrightarrow{AP}=\displaystyle\frac{19}{22}\overrightarrow{x}+\displaystyle\frac{8}{11}\overrightarrow{y}\) ・・・③
次に，点 \(Q\) は直線 \(AP\) 上より，実数 \(k\) を用いて
\(\overrightarrow{AQ}=k\overrightarrow{AP}\) と表せる．
③より，\(\overrightarrow{AQ}=\displaystyle\frac{19k}{22}\overrightarrow{x}+\displaystyle\frac{8k}{11}\overrightarrow{y}\) ・・・④
また，点 \(Q\) は線分 \(BC\) 上より，実数 \(l\) を用いて
\(\overrightarrow{AQ}=\overrightarrow{x}+l\overrightarrow{y}\) ・・・⑤と表せる，
\(\overrightarrow{x}≠\overrightarrow{0}\) , \(\overrightarrow{y}≠\overrightarrow{0}\) , \(\overrightarrow{x}\) と \(\overrightarrow{y}\) が平行でない(\(\overrightarrow{x}\) , \(\overrightarrow{y}\) は一次独立)であるから，③，④より
\(\displaystyle\frac{19k}{22}=1\) \(\iff\) \(k=\displaystyle\frac{22}{19}\)
よって，\(\overrightarrow{AQ}=\displaystyle\frac{22}{19}\overrightarrow{AP}\)
したがって，\(AP : PQ = 19 : 3\)
方針②幾何(相似)を利用した解答
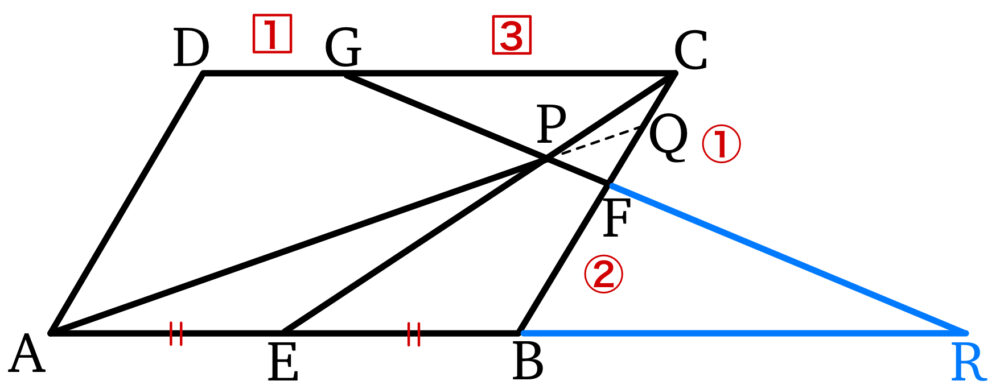
上図のように，直線 \(AB\) と直線 \(GF\) の交点を \(R\) とおく．
このとき，\(\triangle FBR\text{∽}\triangle FCG\) より (※ \(\text{∽}\) は相似)
\(BR : CG = FB : FC = 2 : 1\)
よって，\(BR=2CG\) ・・・①
ここで正の実数 \(a\) を用いて，\(AB=4a\) とおくと，
\(CG=3a\) より，①から \(BR=6a\)
ゆえに \(ER=EB+BR=\displaystyle\frac{1}{2}AB+BR=2a+6a=8a\)
次に\(\triangle PER\text{∽}\triangle PCG\) より
\(PE : PC = ER : CG = 8a : 3a = 8 : 3\)
\(PE:PC=8:3\) とわかったので，\(\overrightarrow{AP}\) がわかるね！
上のように，\(s\) , \(t\) とおいて計算する必要がなくなった！
〇〇の分野だけで解くのではなく，様々な分野の知識を総合して問題にアプローチできるようになりましょう！
コメント