【問題】
\(f(x)=x^3+2x^2+2\) とする.
\(| f(n) |\) と \(| f(n+1) |\) がともに素数となる整数 \(n\) をすべて求めよ.
整数問題のPoint
まず整数問題すべてに共通して言えるPointは
- 積の形に変形
- 条件から範囲を絞る
- 倍数や余りに注目
整数問題の多くが、上の1から3のいずれかで処理できます。
この3つのPointは絶対に頭の中に叩き込んでください!
【考え方・思考の仕方】
《Step1》「素数」は積の形に弱い!
例:仮に素数 \(p\) に対して、\(p=ab\) の形に式変形をすることが出来れば、
\(a=1\) または \(b=1\) である必要がある.※逆の確認が必要!
・素数に関する話&整数問題のPointの1つ目より、\(f(x)=x^3+2x^2+2\) が因数分解したい!という気持ちになって欲しい.
→しかし残念ながら因数分解できず・・・撤退
※今回は結果的にできなかったが、ここでは問題文を見て、どのように思考していくかを大切にしています。考える癖を身に付けて欲しい.
※因数分解が出来ないからこそ次のStepに進める
《Step2》範囲による絞り込み
・範囲を整数問題のPointの2つ目より、条件から範囲を絞りたいが・・・???・・・撤退!!
※しつこいですが、できなかったことを確認することが大切!こうやって1つ1つ考えて、突破口を見出していくことが大切!
《Step3》倍数や余りに注目
・整数問題のPointの3つ目より、倍数や余りに注目!
→とりあえずmod 2、mod 3、mod 4あたりを考えてみよう!
※難関大学では3つ目のPointを使うことが非常に多い!
合同式って何?合同式を復習したい人は「合同式とは?合同式の基本性質を理解し、使えるようにする」と「合同式(基本編)基本的な問題で合同式を使う練習」を参考にしてください。
難関大学を考えている場合、合同式が使えないのは致命傷です!
→mod 2で考えてみる
( ⅰ ) \(n≡0\) のとき
\(f(n)≡0\) 、\(f(n+1)≡f(1)≡5≡1\)
( ⅱ ) \(n≡1\) のとき
\(f(n)≡1\) 、\(f(n+1)≡f(0)≡0\)
→( ⅰ )、( ⅱ )より、mod 2(偶奇) で考えた結果、\(f(n)\)、\(f(n+1)\) の偶奇は一致しない
→\(|f(n)|\)、\(|f(n+1)|\) の一方は偶数
→\(|f(n)|=2\) または \(|f(n+1)|=2\) を考えればよい!
※それぞれ計算しても良いが、2度計算するのは少し大変
→\(|f(x)|=2\) を満たす\(x\) を考えたのち、\(x=n , n+1\)を考える
※難関大学の整数問題は、3つ目のPointを使用することが非常に多い!
【問題】
\(f(x)=x^3+2x^2+2\) とする.
\(| f(n) |\) と \(| f(n+1) |\) がともに素数となる整数 \(n\) をすべて求めよ.
【解答】
法を2として ( mod 2 として ) 考える
( ⅰ ) \(n≡0\) のとき
\(f(n)≡0\) 、\(f(n+1)≡f(1)≡1\)
( ⅱ ) \(n≡1\) のとき
\(f(n)≡1\) 、\(f(n+1)≡f(0)≡0\)
したがって、
\(|f(n)|\)、\(|f(n+1)|\) の一方は偶数、もう一方は奇数.
\(|f(n)|\)、\(|f(n+1)|\) は素数であるから、\(|f(n)|\)、\(|f(n+1)|\) のいずれか一方が2である必要がある.
ここで、\(|f(x)|=2\) を考える.
(ア) \(f(x)=2\) のとき
\(x^3+2x^2+2=2\) より
\(x^3+2x^2=0\)
\(x^2(x+2) =0\)
\(x=0 , -2\)
\(x=n , n+1\) より
\(n=0 , -1 , -2 , -3 \)
\(n=0\) のとき、\(|f(n)|=2 \)、\(|f(n+1)|=5 \) となり条件を満たす.
\(n=-1\) のとき、\(|f(n)|=3 \)、\(|f(n+1)|=2 \) となり条件を満たす.
\(n=-2\) のとき、\(|f(n)|=2 \)、\(|f(n+1)|=3 \) となり条件を満たす.
\(n=-3\) のとき、\(|f(n)|=7 \)、\(|f(n+1)|=2 \) となり条件を満たす.
(イ) \(f(x)=-2\) のとき
\(x^3+2x^2+2=2\) より
\(x^3+2x^2+4=0\)

整数解を持ちそうにない??
方程式の実数解
☞両辺のグラフの交点の\(x\) 座標
ここで\(g(x)= x^3+2x^2+4\) のグラフを考える
\(g^{\prime}(x)=3x^2+4x=x(3x+4)\)
増減表とグラフは以下の通りになり、
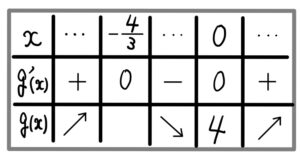
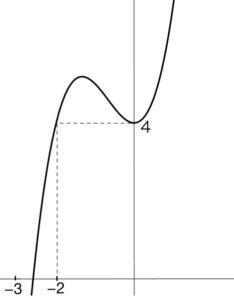
また、\(g(-3)=-5<0\) , \(g(-2)=4>0\) でグラフから
\(g(x)=0\) の実数解は、\(-3<x<-2\) に1つだけ.
つまり\(g(x)=0\) は整数解を持たないので不適
したがって、\(n=0 , -1 , -2 , -3 \)
最後に
いかがだったでしょうか?
ただ解答をなぞって勉強していては、いつまでも整数問題はできるようになりません。
どのように考え、失敗し、次の考え方に至るのかが大切です!
同じ問題は出題されませんが、同じ形式の問題は出題されます!
しっかりと考え方を学び、実力UPを!







コメント