【2021神戸大学(理)】
\(\overrightarrow{0}\) でない \(2\) つのベクトル \(\overrightarrow{a}\) , \(\overrightarrow{b}\) が垂直であるとする.\(\overrightarrow{a}+\overrightarrow{b}\) と \(\overrightarrow{a}+3\overrightarrow{b}\) のなす角を \(\theta\) ( \(0≦\theta≦\pi\) ) とする.以下の問に答えよ.
(1) \(\left|\overrightarrow{a}\right|=x\) , \(\left|\overrightarrow{b}\right|=y\) とするとき,\(\sin^2 \theta\) を \(x\) , \(y\) を用いて表せ.
(2) \(\theta\) の最大値を求めよ.
解答
(1)
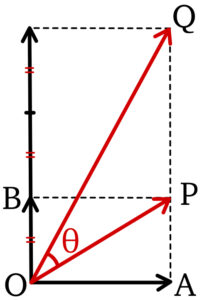
右図のように \(\overrightarrow{a}=\overrightarrow{OA}\) , \(\overrightarrow{b}=\overrightarrow{OB}\) , \(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{OP}\) , \(\overrightarrow{a}+3\overrightarrow{b}=\overrightarrow{OQ}\) とおく.
\(\tan \angle POA=\displaystyle\frac{AP}{OA}=\displaystyle\frac{y}{x}\) ,
\(\tan \angle QOA=\displaystyle\frac{AQ}{OA}=\displaystyle\frac{3y}{x}\) であり,
\(\tan \theta=\tan (\angle QOA-\angle POA)\) より
\(\tan \theta=\displaystyle\frac{\displaystyle\frac{3y}{x}-\displaystyle\frac{y}{x}}{1+\displaystyle\frac{3y}{x}\cdot\displaystyle\frac{y}{x}}\)
よって,\(\tan \theta=\displaystyle\frac{2xy}{x^2+3y^2}\) ・・・①
また,\(\sin^2 \theta+\cos^2 \theta=1\) の両辺を \(\sin^2 \theta\) で割ることで
\(1+\displaystyle\frac{1}{\tan^2 \theta}=\displaystyle\frac{1}{\sin^2 \theta}\) より
\(\sin^2 \theta=\displaystyle\frac{\tan^2 \theta}{1+\tan^2 \theta}\)
①を代入すると
\(\sin^2 \theta=\displaystyle\frac{\left(\displaystyle\frac{2xy}{x^2+3y^2}\right)^2}{1+\left(\displaystyle\frac{2xy}{x^2+3y^2}\right)^2}\)
\(=\displaystyle\frac{4x^2y^2}{(x^2+3y^2)+4x^2y^2}\)
したがって,
\(\sin^2 \theta=\displaystyle\frac{4x^2y^2}{x^4+10x^2y^2+9y^4}\)
(2)
\(x>0\) , \(y>0\) , ①より,\(\tan \theta>0\) であるから,
\(0≦\theta<\displaystyle\frac{\pi}{2}\) ・・・②
(1)より
\(\sin^2 \theta=\displaystyle\frac{4x^2y^2}{x^4+10x^2y^2+9y^4}\) の分母分子を \(x^2y^2\) で割ると
\(\sin^2 \theta=\displaystyle\frac{4}{\displaystyle\frac{x^2}{y^2}+10+\displaystyle\frac{9y^2}{x^2}}\)
相加平均・相乗平均の関係より,
\(\displaystyle\frac{x^2}{y^2}+\displaystyle\frac{9y^2}{x^2}≧2\sqrt{\displaystyle\frac{x^2}{y^2}\cdot\displaystyle\frac{9y^2}{x^2}}=6\)
(等号成立は \(\displaystyle\frac{x^2}{y^2}=\displaystyle\frac{9y^2}{x^2}\) \(\iff\) \(x=\sqrt{3}y\) のとき )
よって,\(\sin^2 \theta=\displaystyle\frac{4}{\displaystyle\frac{x^2}{y^2}+10+\displaystyle\frac{9y^2}{x^2}}≧\displaystyle\frac{4}{16}=\displaystyle\frac{1}{4}\)
②より \(\sin^2 \theta\) が最大のとき \(\theta\) も最大となるため
\(\sin^2 \theta=\displaystyle\frac{1}{4}\) のとき
つまり \(\sin \theta=\displaystyle\frac{1}{2}\) のとき
\(\theta\) の最大値は \(\displaystyle\frac{\pi}{6}\)





コメント
タンジェントの加法定理違くない?
コメントありがとうございます。
符号の間違いがありました。ご指摘ありがとうございます。
先ほど訂正させていただきました。今後ともよろしくお願いします。