【2023北海道大学・理系・第２問】
\(O\) を原点とする座標空間において，\(3\) 点 \(A(4,2,1)\) , \(B(1,-4,1)\) , \(C(2,2,-1)\) を通る平面を \(\alpha\) とおく．また，球面 \(S\) は半径が \(9\) で，\(S\) と \(\alpha\) の交わりは \(A\) を中心とし \(B\) を通る円であるとする．ただし，\(S\) の中心 \(P\) の \(z\) 座標は正とする．
(１) 線分 \(AP\) の長さを求めよ．
(２) \(P\) の座標を求めよ．
(３) \(S\) と直線 \(OC\) は \(2\) 点で交わる．その \(2\) 点間の距離を求めよ．
解答・解説
(１) 線分 \(AP\) の長さを求めよ．
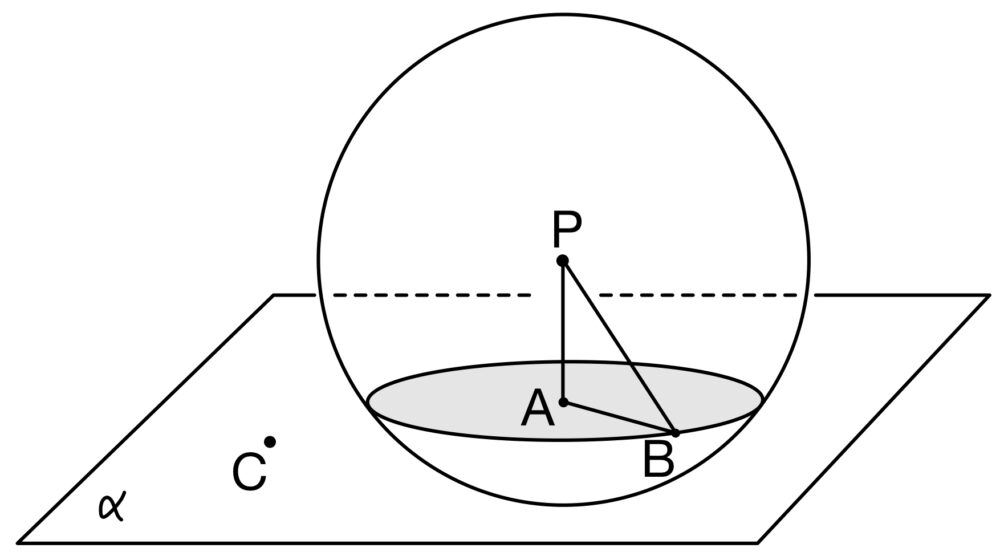\(\overrightarrow{AB}=(-3,-6,0)\)，\(\overrightarrow{AC}=(-2,0,-2)\) で
\(AP\perp\) 平面 \(\alpha\) より三平方の定理から
\(AB^2+AP^2=BP^2\)
\(\left\{(-3)^2+6^2+0^2\right\}+AP^2=9^2\)
\(45+AP^2=81\)
よって，\(AP=6\)
(２) \(P\) の座標を求めよ．
\(P(a,b,c)\) とおく．
\(AP\perp\) 平面 \(\alpha\) より
\(\overrightarrow{AP}\cdot\overrightarrow{AB}=0\) かつ \(\overrightarrow{AP}\cdot\overrightarrow{AC}=0\)
\(\overrightarrow{AP}=(a-4,b-2,c-1)\) より
\(\overrightarrow{AP}\cdot\overrightarrow{AB}=0\)
\(\iff\) \(-3(a-4)-6(b-2)=0\)
\(\iff\) \(a+2b-8=0\) ・・・①
\(\overrightarrow{AP}\cdot\overrightarrow{AC}=0\)
\(\iff\) \(-2(a-4)-2(c-1)=0\)
\(\iff\) \(a+c-5=0\) ・・・②
また(１)より \(AP=6\) より
\((a-4)^2+(b-2)^2+(c-1)^2=36\) ・・・③
①，②，③より
\((a,b,c)=(0,4,5),(8,0,-3)\)
\(P\) の \(z\) 座標は正なので，求める点 \(P(0,4,5)\)
(３) \(S\) と直線 \(OC\) は \(2\) 点で交わる．その \(2\) 点間の距離を求めよ．
球 \(S\) と直線 \(OC\) の交点を \(Q(x,y,z)\) とする．
点 \(Q\) は球 \(S\) 上の点より，\(PQ=9\)
(２)の結果から
\(PQ^2=x^2+(y-4)^2+(z-5)^2=81\) ・・・④
また点 \(Q\) は直線 \(OC\) 上の点より，実数 \(k\) を用いて
\(\overrightarrow{OQ}=k\overrightarrow{OC}\)
\((x,y,z)=k(2,2,-1)=(2k,2k,-k)\) ・・・⑤
④，⑤より
\((2k)^2+(2k-4)^2+(-k-5)^2=81\)
\(9k^2-6k-40=0\)
\(k=\displaystyle\frac{1\pm\sqrt{41}}{3}\)
よって球 \(S\) と直線 \(OC\) の \(2\) 交点を \(Q_{1}\)，\(Q_{2}\) とすると
\(\overrightarrow{OQ_{1}}=\displaystyle\frac{1-\sqrt{41}}{3}(2,2,-1)\)
\(\overrightarrow{OQ_{2}}=\displaystyle\frac{1+\sqrt{41}}{3}(2,2,-1)\)
\(\overrightarrow{Q_{1}Q_{2}}=\displaystyle\frac{2\sqrt{41}}{3}(2,2,-1)\) より
求める \(2\) 点間の距離は
\(\left|\overrightarrow{Q_{1}Q_{2}}\right|=\displaystyle\frac{2\sqrt{41}}{3}\sqrt{2^2+2^2+(-1)^2}=2\sqrt{41}\)
コメント