【2023早稲田大学・教育学部・第１問(３)】
\(x_{0}=0\)，\(y_{0}=-1\) のとき，非負整数 \(n≧0\) に対して，
\(x_{n+1}=\left(\cos\displaystyle\frac{3\pi}{11}\right)x_{n}-\left(\sin\displaystyle\frac{3\pi}{11}\right)y_{n}\)
\(y_{n+1}=\left(\sin\displaystyle\frac{3\pi}{11}\right)x_{n}+\left(\cos\displaystyle\frac{3\pi}{11}\right)y_{n}\)
で定義される数列において，\(x_{n}\) が最小値をとる最初の \(n\) を求めよ．
解答・解説
\(\alpha=\displaystyle\frac{3\pi}{11}\) とおく．
\(x_{n+1}+iy_{n+1}\)
\(=(x_{n}\cos\alpha-y_{n}\sin\alpha)+i(x_{n}\sin\alpha+y_{n}\cos\alpha)\)
\(=x_{n}(\cos\alpha+i\sin\alpha)+iy_{n}(\cos\alpha+i\sin\alpha)\)
\(=(\cos\alpha+i\sin\alpha)(x_{n}+iy_{n})\)
\(=(\cos\alpha+i\sin\alpha)^n(x_{0}+iy_{0})\)
ド・モアブルの定理より
\(x_{n+1}+iy_{n+1}=(\cos\alpha n+i\sin\alpha n)(0-i)\)
\(=\left(\cos\displaystyle\frac{3n\pi}{11}+i\sin\displaystyle\frac{3n\pi}{11}\right)\left\{\cos\left(-\displaystyle\frac{\pi}{2}\right)+i\sin\left(-\displaystyle\frac{\pi}{2}\right)\right\}\)
\(=\cos\left(\displaystyle\frac{3n}{11}-\displaystyle\frac{1}{2}\right)\pi+i\sin\left(\displaystyle\frac{3n}{11}-\displaystyle\frac{1}{2}\right)\pi\)
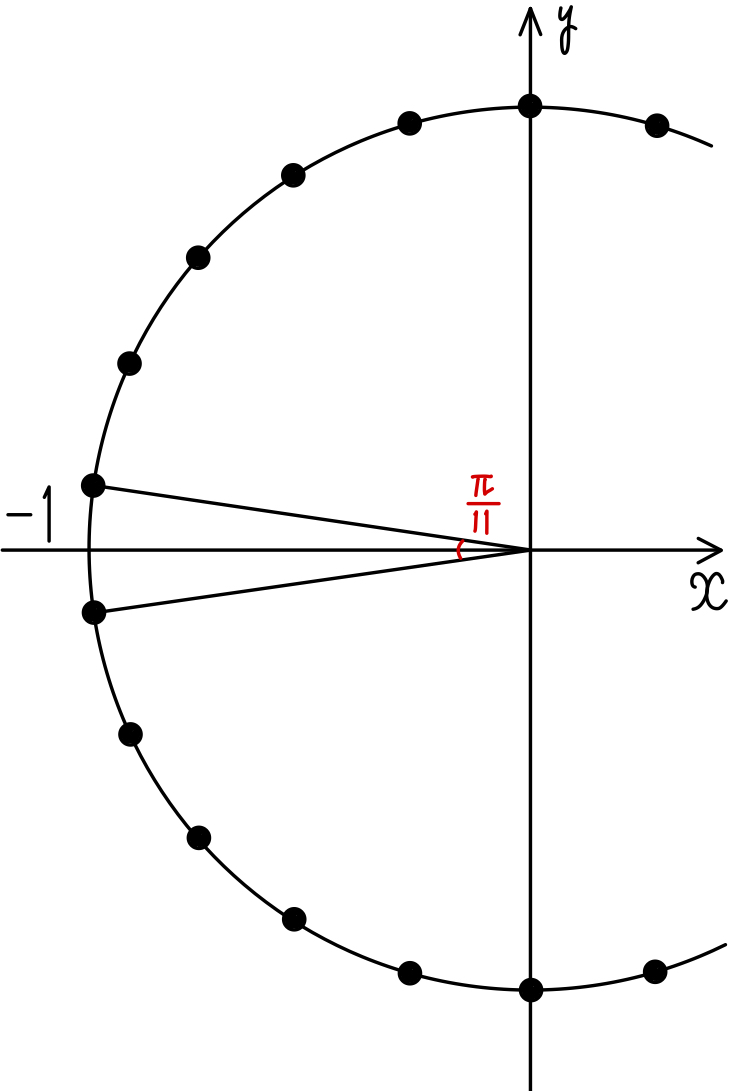よって \((x_{n},y_{n})\) は，単位円の内接する正二十二角形の頂点を動く．
ゆえに，\(x_{n}\) が最小となるのは，自然数 \(m\) を用いて
\(\left(\displaystyle\frac{3n}{11}-\displaystyle\frac{1}{2}\right)\pi=(2m-1)\pi\pm\displaystyle\frac{\pi}{22}\)
となるときである．
\(3n=22m-5\) または \(3n=22m-6\)
\(m=\displaystyle\frac{3n+5}{22},\displaystyle\frac{3n+6}{22}\)
\(n=0,1,2,\cdots\) と小さいものから順に考えると
最小値をとる最初の \(n\) は \(n=13\)
コメント