

(1)開始時刻から1秒後の \(\triangle PBQ\) の面積
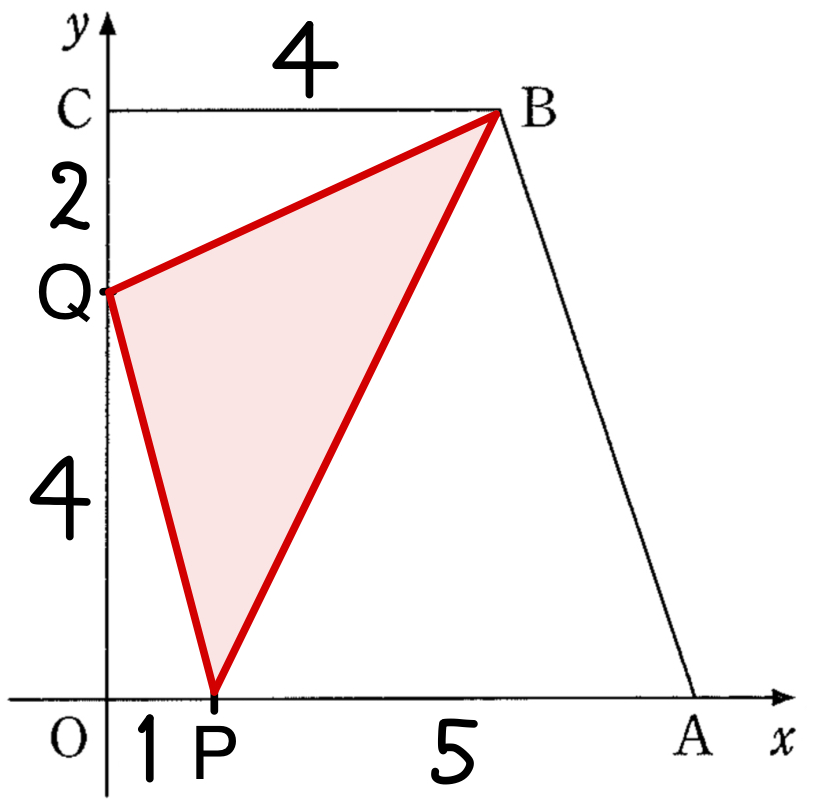 台形 \(OABC\) の面積は,\(\displaystyle\frac{1}{2}\times(4+6)\times 6=30\)
台形 \(OABC\) の面積は,\(\displaystyle\frac{1}{2}\times(4+6)\times 6=30\)
開始時刻から1秒後は,\(OP=1\),\(CQ=2\) で
\(\triangle OPQ=\displaystyle\frac{1}{2}\times 1\times 4=2\)
\(\triangle PAB=\displaystyle\frac{1}{2}\times 5\times 6=15\)
\(\triangle BCQ=\displaystyle\frac{1}{2}\times 4\times 2=4\) より
\(\triangle PBQ=30-(2+15+4)= \)\(9\) ・・・《ア》
(2)開始時刻から3秒間の \(\triangle PBQ\) の面積の最小・最大
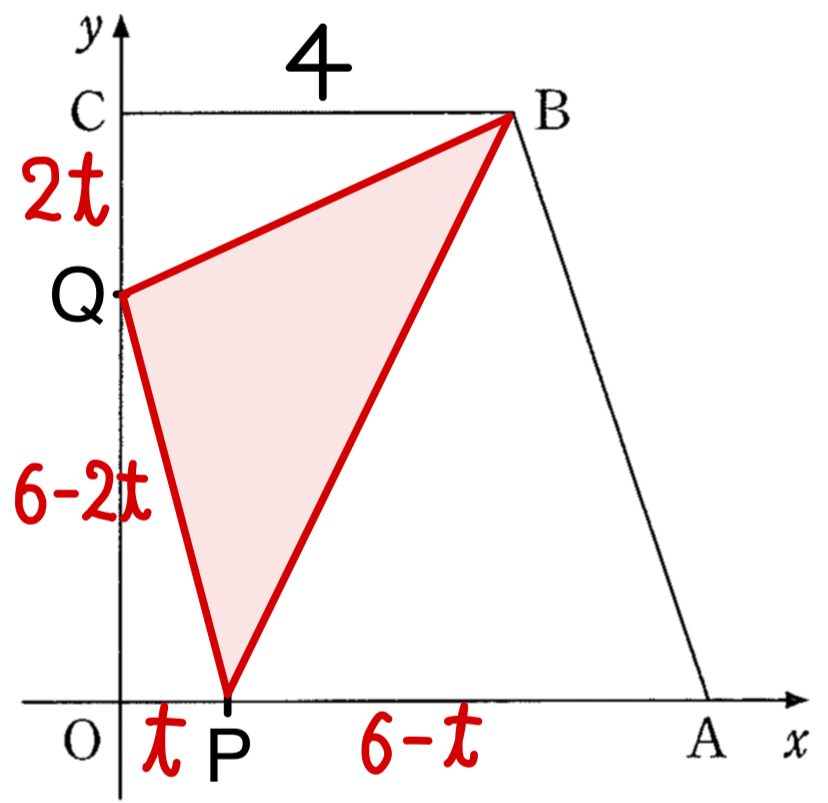 開始時刻から \(t\) 秒後 ( \(0≦t≦3\) ) のとき
開始時刻から \(t\) 秒後 ( \(0≦t≦3\) ) のとき
\(\triangle OPQ=\displaystyle\frac{1}{2}\times t\times (6-2t)=3t-t^2\)
\(\triangle PAB=\displaystyle\frac{1}{2}\times (6-t)\times 6=18-3t\)
\(\triangle BCQ=\displaystyle\frac{1}{2}\times 4\times 2t=4t\) より
\(\triangle PBQ=30-\left\{(3t-t^2)+(18-3t)+4t\right\} \)
 \(=t^2-4t+12\)
\(=t^2-4t+12\)
\(=(t-2)^2+8\)
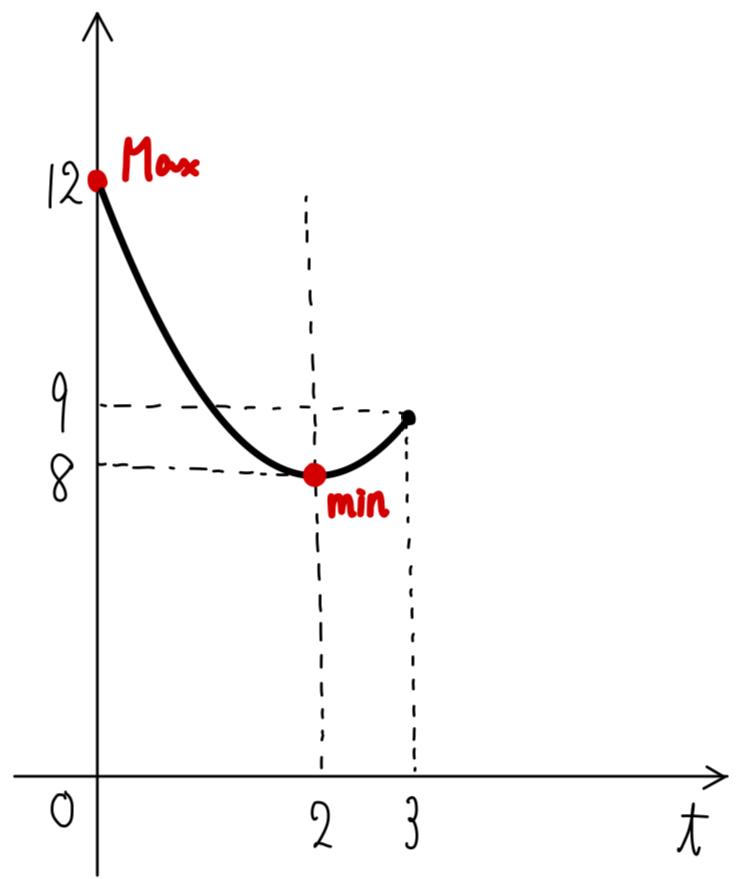
\(0≦t≦3\) における最大値・最小値は
\(t=2\) のとき,最小値:\(8\) ・・・《イ》
\(t=0\) のとき,最大値:\(12\) ・・・《ウエ》
(3)開始時刻から終了時刻までの \(\triangle PBQ\) の面積の最小・最大
\(0≦t≦3\) のとき(2)より
\(\triangle PBQ=(t-2)^2+8\)
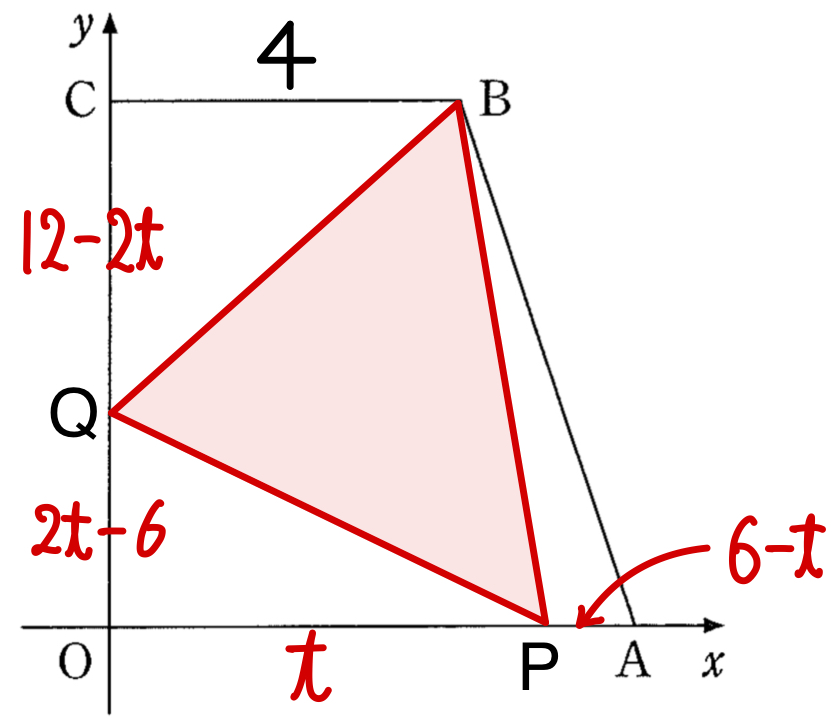 \(3≦t≦6\) のとき
\(3≦t≦6\) のとき
\(\triangle OPQ=\displaystyle\frac{1}{2}\times t\times (2t-6)= t^2-3t\)
\(\triangle PAB=\displaystyle\frac{1}{2}\times (6-t)\times 6=18-3t\)
\(\triangle BCQ=\displaystyle\frac{1}{2}\times 4\times (12-2t)=24-4t\) より
\(\triangle PBQ=30-\left\{(t^2-3t)+(18-3t)+(24-4t)\right\} \)
 \(=-t^2+10t-12\)
\(=-t^2+10t-12\)
\(=-(t-5)^2+13\)
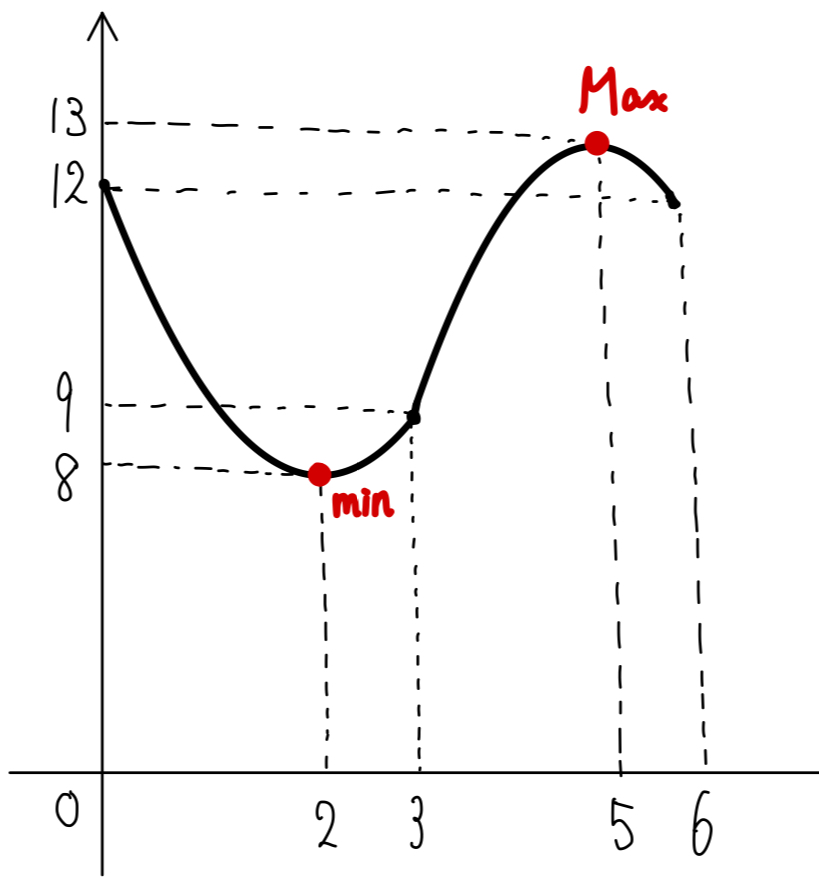
よって,\(0≦t≦6\) における最大値・最小値は
\(t=2\) のとき,最小値:\(8\) ・・・《オ》
\(t=5\) のとき,最大値:\(13\) ・・・《カキ》
(4)開始時刻から終了時刻までの \(\triangle PBQ\) の面積が10以下
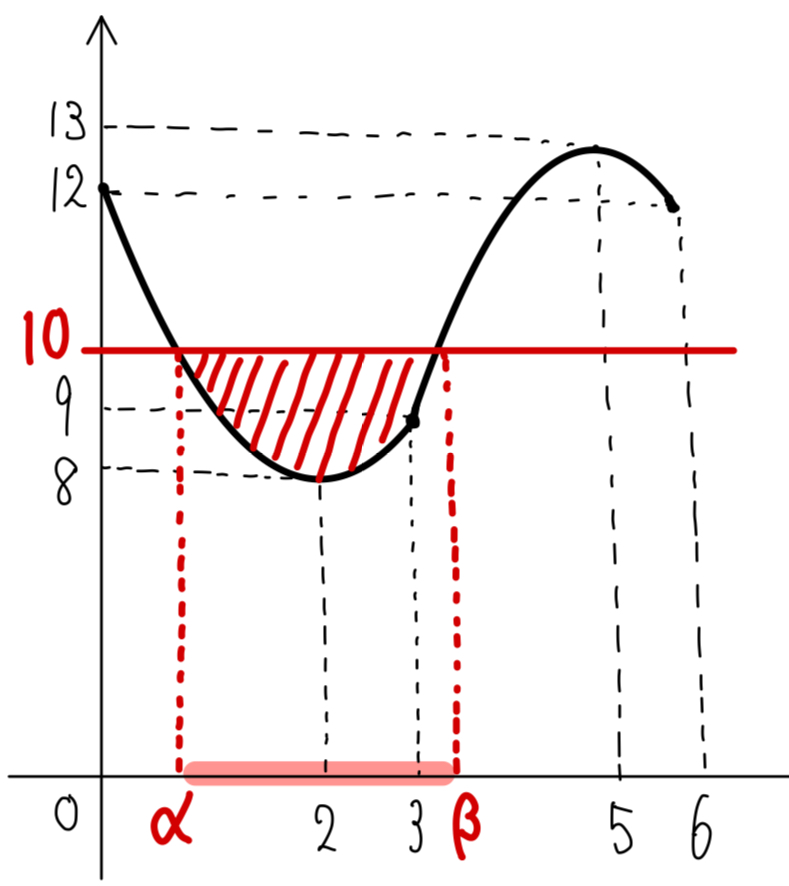 グラフの \(\alpha\) , \(\beta\) を求め,\(\alpha≦t≦\beta\) が条件を満たす時間である.
グラフの \(\alpha\) , \(\beta\) を求め,\(\alpha≦t≦\beta\) が条件を満たす時間である.
\(0≦t≦3\) のとき
\(t^2-4t+12=10\)
\(t^2-4t+2=0\)
\(t=2\pm\sqrt{2}\)
\(0≦t≦3\) より \(\alpha=2-\sqrt{2}\)
\(3≦t≦6\) のとき
\(-t^2+10t-12=10\)
\(t^2-10t+22=0\)
\(t=5\pm\sqrt{3}\)
\(3≦t≦6\) より \(\beta=5+\sqrt{3}\)
よって,\(\triangle PBQ\) の面積が10以下となるのは
\(2-\sqrt{2}≦t≦5+\sqrt{3}\)
したがって,\((5+\sqrt{3})-(2-\sqrt{2})=\)\(3-\sqrt{3}+\sqrt{2}\) 秒間・・・《ク〜コ》







コメント